
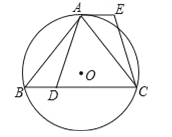
【题目】已知:如图,⊙O是△ABC的外接圆,![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据等弧所对的圆周角相等,得出∠B=∠ACB,再根据全等三角形的判定得△ABD≌△CAE,即可得出AD=CE;
(2)连接AO并延长,交边BC于点H,由等腰三角形的性质和外心的性质得出AH⊥BC,再由垂径定理得BH=CH,得出CG与AE平行且相等.
试题解析:(1)在⊙O中,∵![]() ,∴AB=AC,∴∠B=∠ACB,∵AE∥BC,∴∠EAC=∠ACB,∴∠B=∠EAC,在△ABD和△CAE中,∵AB=CA,∠B=∠EAC,BD=AE,∴△ABD≌△CAE(SAS),∴AD=CE;
,∴AB=AC,∴∠B=∠ACB,∵AE∥BC,∴∠EAC=∠ACB,∴∠B=∠EAC,在△ABD和△CAE中,∵AB=CA,∠B=∠EAC,BD=AE,∴△ABD≌△CAE(SAS),∴AD=CE;
(2)连接AO并延长,交边BC于点H,∵![]() ,OA为半径,∴AH⊥BC,∴BH=CH,∵AD=AG,∴DH=HG,∴BH﹣DH=CH﹣GH,即BD=CG,∵BD=AE,∴CG=AE,∵CG∥AE,∴四边形AGCE是平行四边形.
,OA为半径,∴AH⊥BC,∴BH=CH,∵AD=AG,∴DH=HG,∴BH﹣DH=CH﹣GH,即BD=CG,∵BD=AE,∴CG=AE,∵CG∥AE,∴四边形AGCE是平行四边形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
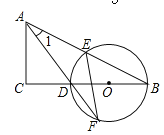
【题目】如图,在△ABC中,∠C=90°,D是BC边上一点,以DB为直径的⊙O经过AB的中点E,交AD的延长线于点F,连结EF.
(1)求证:∠1=∠F;
(2)若sinB=![]() ,EF=
,EF=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为 x ( x 大于0)秒.![]()
(1)点C表示的数是;
(2)当 ![]() 秒时,点P到达点A处?
秒时,点P到达点A处?
(3)运动过程中点P表示的数是(用含字母 ![]() 的式子表示);
的式子表示);
(4)当P,C之间的距离为2个单位长度时,求 x 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
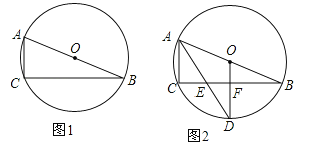
【题目】已知⊙O为△ABC的外接圆,圆心O在AB上.
(1)在图1中,用尺规作图作∠BAC的平分线AD交⊙O于D(保留作图痕迹,不写作法与证明);
(2)如图2,设∠BAC的平分线AD交BC于E,⊙O半径为5,AC=4,连接OD交BC于F.
①求证:OD⊥BC;
②求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F在函数y= ![]() (x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)
(x>0)的图象上,直线EF分别与x轴、y轴交于点A,B,且BE:BF=1:m.过点E作EP⊥y轴于P,已知△OEP的面积为1,则k值是 , △OEF的面积是(用含m的式子表示)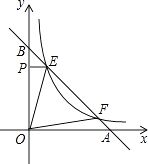
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度约为( )(精确到0.1米,参考数据:
,则大楼AB的高度约为( )(精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
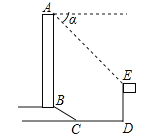
A.30.6 B.32.1 C.37.9 D.39.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2﹣6x﹣8=0,下列变形正确的是( )
A. (x﹣6)2=﹣8+36 B. (x﹣6)2=8+36 C. (x﹣3)2=8+9 D. (x﹣3)2=﹣8+9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com