
【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为 x ( x 大于0)秒.![]()
(1)点C表示的数是;
(2)当 ![]() 秒时,点P到达点A处?
秒时,点P到达点A处?
(3)运动过程中点P表示的数是(用含字母 ![]() 的式子表示);
的式子表示);
(4)当P,C之间的距离为2个单位长度时,求 x 的值.
【答案】
(1)1
(2)5
(3)![]() ?4+2x
?4+2x
(4)解:①当点P在点C左边时,
∵P、C之间的距离为2个单位长度,
∴点P表示的数为-1,
∴2x-4=-1,
∴x=![]() .
.
②当点P在点C右边时,
∵P、C之间的距离为2个单位长度,
∴点P表示的数为3,
∴2x-4=3,
∴x=![]() .
.
综上所述:当x=![]() 或
或![]() 时,P,C之间的距离为2个单位长度.
时,P,C之间的距离为2个单位长度.
【解析】解:(1)∵点C到点A、点B的距离相等,
∴C为AB的中点,
∴点C表示的数为:![]() =1.
=1.
所以答案是:1.
(2)依题可得:
AB=6-(-4)=10,
∴10÷2=5(秒).
答:但x为5秒时,点P到达点A处.
(3)依题可得:
运动过程中点P表示的数为:-4+2x.
所以答案是:2x-4.
【考点精析】本题主要考查了数轴的相关知识点,需要掌握数轴是规定了原点、正方向、单位长度的一条直线才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
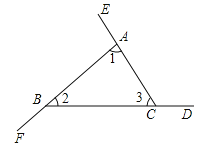
【题目】用两种方法证明“三角形的外角和等于360°”.
如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证∠BAE+∠CBF+∠ACD=360°.
证法1:∵ ,∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵ ,∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象都经过点A(m,2).
)的图象都经过点A(m,2).

(1)求点A的坐标及反比例函数的表达式;
(2)设一次函数![]() 的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司要把3000吨货物从M市运到W市.(每日的运输量为固定值)
(1)从运输开始,每天运输的货物吨数y(单位:吨)与运输时间x(单位:天)之间有怎样的函数关系式?
(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务,求原计划完成运输任务的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于⊙O,A是![]() 的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且![]() .
.
(1)求证:△ADC∽△EBA;
(2)如果AB=8,CD=5,求tan∠CAD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
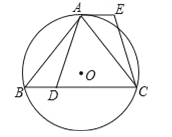
【题目】已知:如图,⊙O是△ABC的外接圆,![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
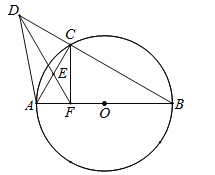
【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.
(1)求证:△DFB是等腰三角形;
(2)若DA=![]() AF,求证:CF⊥AB.
AF,求证:CF⊥AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com