【题目】解不等式组 
，并把不等式①和②的解集在同一数轴上表示出来．
【答案】解： 
，
由不等式①，得x＞﹣1，
由不等式②，得x≤4，
∴原不等式组的解集是﹣1＜x≤4，在数轴上表示如下图所示，
．
【解析】t通过移项、合并同类项，由求不等式解集口诀“大小小大”可求出.
【考点精析】掌握不等式的解集在数轴上的表示和一元一次不等式组的解法是解答本题的根本，需要知道不等式的解集可以在数轴上表示，分三步进行：①画数轴②定界点③定方向．规律：用数轴表示不等式的解集，应记住下面的规律：大于向右画，小于向左画，等于用实心圆点，不等于用空心圆圈；解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，以AC为直径的⊙O交BC于点D，
交AB于点E，过点D作DF⊥AB，垂足为F，连接DE．
（1）求证：直线DF与⊙O相切；
（2）若AE=7，BC=6，求AC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】用两种方法证明“三角形的外角和等于360°”．
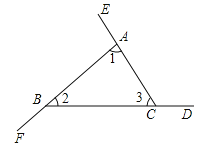
如图，∠BAE、∠CBF、∠ACD是△ABC的三个外角．
求证∠BAE+∠CBF+∠ACD=360°．
证法1：∵ ，∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣（∠1+∠2+∠3）．
∵ ，∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°．
请把证法1补充完整，并用不同的方法完成证法2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D．DF⊥AC，垂足为F，DE⊥BC，垂足为E．给出下列4个结论：①CE=CF；②∠ACB=∠EDF；③DE是⊙O的切线；④
．其中一定成立的是（ ）
A．①②③ B．②③④ C．①③④ D．①②④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】以下问题，不适合用普查的是（ ）
A. 旅客上飞机前的安检 B. 为保证“神州9号”的成功发射，对其零部件进行检查
C. 了解某班级学生的课外读书时间 D. 了解一批灯泡的使用寿命
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数
的图象与反比例函数
（
为常数，且
）的图象都经过点A（m，2）．
（1）求点A的坐标及反比例函数的表达式；
（2）设一次函数的图象与x轴交于点B，若点P是x轴上一点，且满足△ABP的面积是2，直接写出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
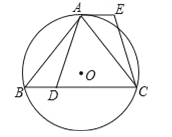
【题目】已知：如图，⊙O是△ABC的外接圆，
，点D在边BC上，AE∥BC，AE=BD．
（1）求证：AD=CE；
（2）如果点G在线段DC上（不与点D重合），且AG=AD，求证：四边形AGCE是平行四边形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com