
【题目】(2016山西省)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg﹣5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货.
方案B:每千克5元,客户需支付运费2000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

科目:初中数学 来源: 题型:
【题目】已知:![]() ,OB,OM,ON是
,OB,OM,ON是![]() 内的射线.
内的射线.
![]() 如图1,若OM平分
如图1,若OM平分![]() ,ON平分
,ON平分![]() 当射线OB绕点O在
当射线OB绕点O在![]() 内旋转时,
内旋转时,![]() ______度
______度![]()
![]() 也是
也是![]() 内的射线,如图2,若
内的射线,如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ,当
,当![]() 绕点O在
绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小.
的大小.
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,当
,当![]() 在
在![]() 绕O点以每秒
绕O点以每秒![]() 的速度逆时针旋转t秒,如图3,若
的速度逆时针旋转t秒,如图3,若![]() :
:![]() :3,求t的值.
:3,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
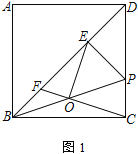
【题目】已知:在正方形ABCD中,AB=6,P为边CD上一点,过P点作PE⊥BD于点E,连接BP.
(1)O为BP的中点,连接CO并延长交BD于点F
①如图1,连接OE,求证:OE⊥OC;
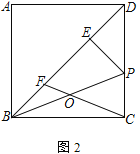
②如图2,若![]() ,求DP的长;
,求DP的长;
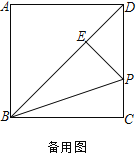
(2)![]() =___________
=___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B,C,D四个点不在同一直线上,根据下列语句画图.
(1)画射线AB,画直线AC,画线段AD;
(2)连接BD与直线AC相交于点E;
(3)延长线段BC,反向延长线段DC;
(4)若在上述所画的图形中,设从点D到点C有四条路径,它们分别是①D→A→B→C;②D→B→C;③D→E→C;④D→C;哪条道路最短?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
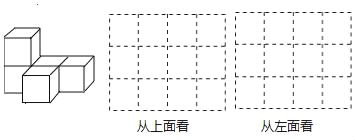
【题目】由大小相同的小立方块搭成的几何体如左图:
(1)请在下面的方格中画出该几何体从上面和从左面看的两个图形.
(2)若现在你手头上还有一些相同的小立方块,如果保持从上面看和从左面看所得图形不变,则在左图中最多可以再添加 个小立方块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若关于x的方程2x﹣3=1和![]() =k﹣3x有相同的解,求k的值
=k﹣3x有相同的解,求k的值
(2)阅读材料:解方程组![]() 时,可由①得x﹣y=1③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得
时,可由①得x﹣y=1③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得![]() ,这种方法被称为“整体代入法”,请用上述方法解方程组
,这种方法被称为“整体代入法”,请用上述方法解方程组 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.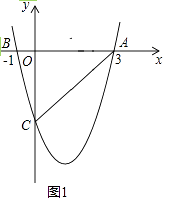
(1)求该二次函数的解析式及点C的坐标;
(2)设该抛物线的顶点为D,求△ACD的面积;
(3)若点P,Q同时从A点出发,如图2(注:图2与图1完全相同),都以每秒1个单位长度的速度分别沿线段AB,AC运动,当其中一点到达终点时,另一点也随之停止运动,当P,Q运动到t秒时,将△APQ沿PQ所在直线翻折,点A恰好落在抛物线上E处,判定此时四边形APEQ的形状,说明理由,并求出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某路公交车从起点经过A、B、C、D站到达终点,一路上下乘客如下表所示。(用正数表示上车的人数,负数表示下车的人数)

(1)到终点下车还有________人.
(2)车行驶在那两站之间车上的乘客最多?________站和________站
(3)若每人乘坐一站需买票1元,问该车出车一次能收入多少钱?写出算式。
查看答案和解析>>
科目:初中数学 来源: 题型:
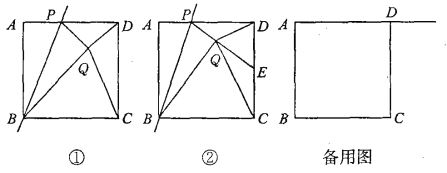
【题目】如图①,已知正方形ABCD的边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连接PQ、DQ、CQ、BQ,设AP=x.
(1)BQ+DQ的最小值是_______,此时x的值是_______;
(2)如图②,若PQ的延长线交CD边于点E,并且∠CQD=90°.
①求证:点E是CD的中点; ②求x的值.
(3)若点P是射线AD上的一个动点,请直接写出当△CDQ为等腰三角形时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com