
ЎѕМвДїЎїИзНј1Ј¬¶юґОєЇКэy=ax2+bx©Ѓ4ЈЁaЎЩ0Ј©µДНјПуУлxЦбЅ»УЪAЈЁ3Ј¬0Ј©Ј¬BЈЁ©Ѓ1Ј¬0Ј©БЅµгЈ¬УлyЦбЅ»УЪµгCЈ®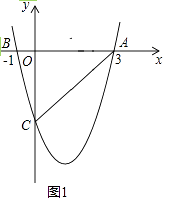
ЈЁ1Ј©ЗуёГ¶юґОєЇКэµДЅвОцКЅј°µгCµДЧш±кЈ»
ЈЁ2Ј©ЙиёГЕЧОпПЯµД¶ҐµгОЄDЈ¬ЗуЎчACDµДГж»эЈ»
ЈЁ3Ј©ИфµгPЈ¬QН¬К±ґУAµгіц·ўЈ¬ИзНј2ЈЁЧўЈєНј2УлНј1НкИ«ПаН¬Ј©Ј¬¶јТФГїГл1ёцµҐО»і¤¶ИµДЛЩ¶И·Ц±рСШПЯ¶ОABЈ¬ACФЛ¶ЇЈ¬µ±ЖдЦРТ»µгµЅґпЦХµгК±Ј¬БнТ»µгТІЛжЦ®НЈЦ№ФЛ¶ЇЈ¬µ±PЈ¬QФЛ¶ЇµЅtГлК±Ј¬Ѕ«ЎчAPQСШPQЛщФЪЦ±ПЯ·ХЫЈ¬µгAЗЎєГВдФЪЕЧОпПЯЙПEґ¦Ј¬ЕР¶ЁґЛК±ЛД±ЯРОAPEQµДРОЧґЈ¬ЛµГчАнУЙЈ¬ІўЗуіцµгEµДЧш±кЈ®
Ўѕґр°ёЎї
ЈЁ1Ј©
ЅвЈє°СµгAЈЁ3Ј¬0Ј©Ј¬BЈЁ©Ѓ1Ј¬0Ј©ґъИлy=ax2+bx©Ѓ4ЈЁaЎЩ0Ј©µГЈє
![]() Ј¬
Ј¬
ЅвµГЈє 
ЈЁ2Ј©
ЅвЈє№эµгDЧчDMЎНyЦбУЪµгMЈ¬

ЎЯy= ![]() x2©Ѓ
x2©Ѓ ![]() x©Ѓ4=
x©Ѓ4= ![]() ЈЁx©Ѓ1Ј©2©Ѓ
ЈЁx©Ѓ1Ј©2©Ѓ ![]() Ј¬
Ј¬
ЎаµгDЈЁ1Ј¬©Ѓ ![]() Ј©ЎўµгCЈЁ0Ј¬©Ѓ4Ј©Ј¬
Ј©ЎўµгCЈЁ0Ј¬©Ѓ4Ј©Ј¬
ФтSЎчACD=SМЭРОAOMD©ЃSЎчCDM©ЃSЎчAOC
= ![]() ЎБЈЁ1+3Ј©ЎБ
ЎБЈЁ1+3Ј©ЎБ ![]() ©Ѓ
©Ѓ ![]() ЎБЈЁ
ЎБЈЁ ![]() ©Ѓ4Ј©ЎБ1©Ѓ
©Ѓ4Ј©ЎБ1©Ѓ ![]() ЎБ3ЎБ4
ЎБ3ЎБ4
=4
ЈЁ3Ј©
ЅвЈєЛД±ЯРОAPEQОЄБвРОЈ¬EµгЧш±кОЄЈЁ©Ѓ ![]() Ј¬©Ѓ
Ј¬©Ѓ ![]() Ј©Ј®АнУЙИзПВ
Ј©Ј®АнУЙИзПВ
ИзНј2Ј¬Eµг№ШУЪPQУлAµг¶ФіЖЈ¬№эµгQЧчЈ¬QFЎНAPУЪFЈ¬

ЎЯAP=AQ=tЈ¬AP=EPЈ¬AQ=EQ
ЎаAP=AQ=QE=EPЈ¬
ЎаЛД±ЯРОAQEPОЄБвРОЈ¬
ЎЯFQЎОOCЈ¬
Ўа ![]() =
= ![]() =
= ![]() Ј¬
Ј¬
Ўа ![]() =
= ![]() =
= ![]()
ЎаAF= ![]() tЈ¬FQ=
tЈ¬FQ= ![]() t
t
ЎаQЈЁ3©Ѓ ![]() tЈ¬©Ѓ
tЈ¬©Ѓ ![]() tЈ©Ј¬
tЈ©Ј¬
ЎЯEQ=AP=tЈ¬
ЎаEЈЁ3©Ѓ ![]() t©ЃtЈ¬©Ѓ
t©ЃtЈ¬©Ѓ ![]() tЈ©Ј¬јґEЈЁ3©Ѓ
tЈ©Ј¬јґEЈЁ3©Ѓ ![]() tЈ¬©Ѓ
tЈ¬©Ѓ ![]() tЈ©Ј¬
tЈ©Ј¬
ЎЯEФЪ¶юґОєЇКэy= ![]() x2©Ѓ
x2©Ѓ ![]() x©Ѓ4ЙПЈ¬
x©Ѓ4ЙПЈ¬
Ўа©Ѓ ![]() t=
t= ![]() ЈЁ3©Ѓ
ЈЁ3©Ѓ ![]() tЈ©2©Ѓ
tЈ©2©Ѓ ![]() ЈЁ3©Ѓ
ЈЁ3©Ѓ ![]() tЈ©©Ѓ4Ј¬
tЈ©©Ѓ4Ј¬
Ўаt= ![]() Ј¬»тt=0ЈЁУлAЦШєПЈ¬ЙбИҐЈ©Ј¬
Ј¬»тt=0ЈЁУлAЦШєПЈ¬ЙбИҐЈ©Ј¬
Фт3©Ѓ ![]() t=©Ѓ
t=©Ѓ ![]() Ј¬©Ѓ
Ј¬©Ѓ ![]() t=©Ѓ
t=©Ѓ ![]() Ј¬
Ј¬
ЎаEЈЁ©Ѓ ![]() Ј¬©Ѓ
Ј¬©Ѓ ![]() Ј©
Ј©
ЎѕЅвОцЎїЈЁ1Ј©Ѕ«AЈ¬BµгЧш±кґъИлєЇКэy=ax2+bx©Ѓ4ЦРЈ¬ЗуµГbЎўaЈ¬Ѕш¶шїЙЗуЅвОцКЅЈ»ЈЁ2Ј©УЙЅвОцКЅПИЗуµГµгDЎўCЧш±кЈ¬ФЩёщѕЭSЎчACD=SМЭРОAOMD©ЃSЎчCDM©ЃSЎчAOC Ј¬ БРКЅјЖЛгјґїЙЈ»ЈЁ3Ј©ЧўТвµЅPЈ¬QФЛ¶ЇЛЩ¶ИПаН¬Ј¬ФтЎчAPQФЛ¶ЇК±¶јОЄµИСьИэЅЗРОЈ¬УЦУЙAЎўE¶ФіЖЈ¬ФтAP=EPЈ¬AQ=EQЈ¬ТЧµГЛД±ЯРОЛД±Я¶јПаµИЈ¬јґБвРОЈ®АыУГБвРО¶Ф±ЯЖЅРРЗТПаµИµДРФЦКїЙУГt±нКѕEµгЧш±кЈ¬УЦEФЪ¶юґОєЇКэµДНјПуЙПЈ¬ЛщТФґъИлјґїЙЗуtЈ¬Ѕш¶шEїЙ±нКѕЈ®
Ўѕїјµгѕ«ОцЎїИПХжЙуМвЈ¬КЧПИРиТЄБЛЅв¶юґОєЇКэµДНјПу(¶юґОєЇКэНјПс№ШјьµгЈє1ЎўїЄїЪ·ЅПт2Ўў¶ФіЖЦб 3Ўў¶Ґµг 4ЎўУлxЦбЅ»µг 5ЎўУлyЦбЅ»µг)Ј¬»№ТЄХЖОХ¶юґОєЇКэµДРФЦК(ФцјхРФЈєµ±a>0К±Ј¬¶ФіЖЦбЧу±ЯЈ¬yЛжxФцґу¶шјхРЎЈ»¶ФіЖЦбУТ±ЯЈ¬yЛжxФцґу¶шФцґуЈ»µ±a<0К±Ј¬¶ФіЖЦбЧу±ЯЈ¬yЛжxФцґу¶шФцґуЈ»¶ФіЖЦбУТ±ЯЈ¬yЛжxФцґу¶шјхРЎ)µДПа№ШЦЄК¶ІЕКЗґрМвµД№ШјьЈ®


 РВїО±кН¬ІЅСµБ·ПµБРґр°ё
РВїО±кН¬ІЅСµБ·ПµБРґр°ё Т»ПЯГыК¦їЪЛгУ¦УГМвМмМмБ·Т»±ѕИ«ПµБРґр°ё
Т»ПЯГыК¦їЪЛгУ¦УГМвМмМмБ·Т»±ѕИ«ПµБРґр°ё СѧѧϰєГ°пКЦПµБРґр°ё
СѧѧϰєГ°пКЦПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪЎчABCЦРЈ¬ЎПABC=45ЎгЈ¬ADЎНBCУЪµгDЈ¬µгEФЪADЙПЈ¬ЗТDE=DCЈ® 
ЈЁ1Ј©ЗуЦ¤ЈєЎчBDEЎХЎчADCЈ»
ЈЁ2Ј©ИфBC=8.4Ј¬tanC= ![]() Ј¬ЗуDEµДі¤Ј®
Ј¬ЗуDEµДі¤Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїУЙґуРЎПаН¬µДРЎБў·ЅїйґоіЙµДјёєОМеИзЧуНјЈє
ЈЁ1Ј©ЗлФЪПВГжµД·ЅёсЦР»іцёГјёєОМеґУЙПГжєНґУЧуГжїґµДБЅёцНјРОЈ®
ЈЁ2Ј©ИфПЦФЪДгКЦН·ЙП»№УРТ»Р©ПаН¬µДРЎБў·ЅїйЈ¬Из№ы±ЈіЦґУЙПГжїґєНґУЧуГжїґЛщµГНјРОІ»±дЈ¬ФтФЪЧуНјЦРЧо¶аїЙТФФЩМнјУЎЎ ЎЎёцРЎБў·ЅїйЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЈЁ2016ЙЅОчКЎЈ©ОТКЎДіЖ»№ы»щµШПъКЫУЕЦКЖ»№ыЈ¬ёГ»щµШ¶ФРиТЄЛН»хЗТ№єВтБїФЪ2000kg©Ѓ5000kgЈЁє¬2000kgєН5000kgЈ©µДїН»§УРБЅЦЦПъКЫ·Ѕ°ёЈЁїН»§Ц»ДЬСЎФсЖдЦРТ»ЦЦ·Ѕ°ёЈ©Јє
·Ѕ°ёAЈєГїЗ§їЛ5.8ФЄЈ¬УЙ»щµШГв·СЛН»хЈ®
·Ѕ°ёBЈєГїЗ§їЛ5ФЄЈ¬їН»§РиЦ§ё¶ФЛ·С2000ФЄЈ®
ЈЁ1Ј©Зл·Ц±рРґіц°ґ·Ѕ°ёAЈ¬·Ѕ°ёB№єВтХвЦЦЖ»№ыµДУ¦ё¶їоyЈЁФЄЈ©Ул№єВтБїxЈЁkgЈ©Ц®јдµДєЇКэ±нґпКЅЈ»
ЈЁ2Ј©Зу№єВтБїxФЪКІГґ·¶О§К±Ј¬СЎУГ·Ѕ°ёA±И·Ѕ°ёBё¶їоЙЩЈ»
ЈЁ3Ј©ДіЛ®№ыЕъ·ўЙМјЖ»®УГ20000ФЄЈ¬СЎУГХвБЅЦЦ·Ѕ°ёЦРµДТ»ЦЦЈ¬№єВтѕЎїЙДЬ¶аµДХвЦЦЖ»№ыЈ¬ЗлЦ±ЅУРґіцЛыУ¦СЎФсДДЦЦ·Ѕ°ёЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎї6ФВ5ИХКЗЎ°КАЅз»·ѕіИХЎ±Ј¬ДПДюКРДіРЈѕЩРРБЛЎ°ВМЙ«јТФ°Ў±СЭЅІ±ИИьЈ¬ИьєуХыАнІОИьН¬С§µДіЙјЁЈ¬ЦЖЧчіЙЦ±·ЅНј(ИзНј)Ј®
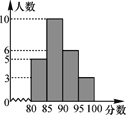
(1)И«РЈ№ІУР¶аЙЩИЛІОјУ±ИИьЈї
(2)ЧйѕаКЗ¶аЙЩЈїЧйКэКЗ¶аЙЩЈї
(3)·ЦКэ¶ОФЪДДёц·¶О§ДЪµДИЛКэЧо¶аЈїІўЗуіцёГРЎЧйµДЖµКэЎўЖµВКЈ»
(4)Из№ы±ИИьіЙјЁ90·ЦТФЙП(є¬90·Ц)їЙТФ»сµГЅ±АшЈ¬ДЗГґ»сЅ±ВККЗ¶аЙЩЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїПВБРёчЧйКэЦРЈ¬ТФЛьГЗОЄ±Яі¤µДПЯ¶ОІ»ДЬ№№іЙЦ±ЅЗИэЅЗРОµДКЗ ЈЁ Ј©
A. 3, 4, 5 B. ![]() C. 30, 40, 50 D. 0.3, 0.4, 0.5
C. 30, 40, 50 D. 0.3, 0.4, 0.5
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЦР№ъѕјГµДїмЛЩ·ўХ№ИГЦЪ¶а№ъјТёРКЬµЅБЛНюРІЈ¬ЛжЧЕµцУгµєКВјюЎўДПєЈОЈ»ъЎўИшµВИлє«µИТ»ПµБРКВјюµД·ўЙъЈ¬№ъјТ°ІИ«Т»ФЩКЬµЅНюРІЈ¬ЛщОЅЎ°№ъјТРЛНцЈ¬ЖҐ·тУРФрЎ±Ј¬ДіРЈ»эј«їЄХ№№ъ·АЦЄК¶ЅМУэЈ¬ѕЕДкј¶јЧЎўТТБЅ°а
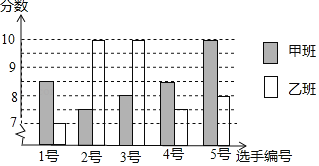
·Ц±рСЎ5ГыН¬С§ІОјУЎ°№ъ·АЦЄК¶Ў±±ИИьЈ¬
ЖдФ¤ИьіЙјЁИзНјЛщКѕЈє
ЈЁ1Ј©ёщѕЭЙПНјМоРґПВ±нЈє
ЖЅѕщКэ | ЦРО»Кэ | ЦЪКэ | |
јЧ°а | 8.5 | 8.5 | ЎЎ ЎЎ |
ТТ°а | 8.5 | ЎЎ ЎЎ | 10 |
ЈЁ2Ј©·Ц±рЗујЧТТБЅ°аµД·ЅІоЈ¬ІўґУОИ¶ЁРФЙП·ЦОцДДёц°аµДіЙјЁЅПєГЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЛжЧЕОТ№ъµД·ўХ№УлЗїґуЈ¬ЦР№ъОД»ЇУлКАЅзёч№ъОД»ЇµДЅ»БчУлИЪєПЅшТ»ІЅјУЗїЈ®ОЄБЛФцЅшКАЅзёч№ъИЛГс¶ФЦР№ъУпСФєНОД»ЇµДАнЅвЈ¬ФЪКАЅзёч№ъЅЁБўїЧЧУС§ФєЈ¬НЖ№гєєУпЈ¬ґ«ІҐЦР»ЄОД»ЇЈ®Н¬К±Ј¬ёч№ъѧУ֮јдµДЅ»Бч»о¶ЇТІЦрДкФцјУЈ®ФЪУл№ъјКУСєГѧУЅ»Бч»о¶ЇЦРЈ¬РЎГфґтЛгЦЖЧцТ»ёцХэ·ЅМеАсєРЛНёшНв№ъЕуУСЈ¬ГїёцГжЙП·Ц±рКйРґТ»ЦЦЦР»Єґ«НіГАµВЈ¬Т»№ІУРЎ°ИКТеАсЦЗРЕРўЎ±БщёцЧЦЈ®ИзНјКЗЛэЙијЖµДАсєРЖЅГжХ№їЄНјЈ¬ДЗГґЎ°АсЎ±ЧЦ¶ФГжµДЧЦКЗЈЁЎЎЎЎЈ©
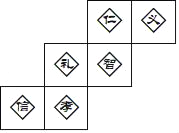
A. ИК B. Те C. ЦЗ D. РЕ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЄБЛМбёЯЙнМеЛШЦКЈ¬УРР©ИЛСЎФсµЅЧЁТµµДЅЎЙнЦРРД¶НБ¶ЙнМеЈ¬ДіЅЎЙнЦРРДµДПы·С·ЅКЅИзПВЈє
Пы·СїЁ | Пы·С·ЅКЅ |
ЖХНЁїЁ | 35ФЄ/ґО |
°ЧЅрїЁ | 280ФЄ/ХЕЈ¬ЖѕїЁГв·СПы·С10ґОФЩЛН2ґО |
ЧкКЇїЁ | 560ФЄ/ХЕЈ¬ЖѕїЁГїґОПы·СІ»ФЩКХ·С |
ТФЙППы·СїЁК№УГДкПЮѕщОЄТ»ДкЈ¬ГїО»№ЛїНЦ»ДЬ№єВтТ»ХЕїЁЈ¬ЗТЦ»ПЮ±ѕИЛК№УГ
ЈЁўсЈ©ИфГїДкИҐёГЅЎЙнЦРРД6ґОЈ¬У¦СЎФсДДЦЦПы·С·ЅКЅёьєПЛгЈї
ЈЁўтЈ©ЙиТ»ДкДЪИҐёГЅЎЙнЦРРДЅЎЙнxґОЈЁxОЄХэХыКэЈ©Ј¬ЛщРиЧЬ·СУГОЄyФЄЈ¬Зл·Ц±рРґіцСЎФсЖХНЁПы·СєН°ЧЅрїЁПы·СµДyУлxµДєЇКэ№ШПµКЅЈ»
ЈЁўуЈ©ИфДіО»№ЛїНГїДкИҐёГЅЎЙнЦРРДЅЎЙнЦБЙЩ18ґОЈ¬ЗлНЁ№эјЖЛг°пЦъХвО»№ЛїНСЎФсЧоєПЛгµДПы·С·ЅКЅЈ®
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com