
【题目】如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
(1) ①依题意补全图形;
②求证:BE⊥AC.
(2)请探究线段BE,AD,CN所满足的等量关系,并证明你的结论.
(3)设AB=1,若点M沿着线段CD从点C运动到点D,则在该运动过程中,线段EN所扫过的面积为______________(直接写出答案).

【答案】(1)①补图见解析;②证明见解析;(2)2BE=![]() AD+CN,证明见解析;(3)
AD+CN,证明见解析;(3)![]() .
.
【解析】(1)①依照题意补全图形即可;②连接CE,由正方形以及等腰直角三角形的性质可得出∠ACD=∠MCN=45°,从而得出∠ACN=90°,再根据直角三角形的性质以及点E为AN的中点即可得出AE=CE,由此即可得出B、E在线段AC的垂直平分线上,由此即可证得BE⊥AC;
(2)BE=![]() AD+
AD+![]() CN.根据正方形的性质可得出BF=
CN.根据正方形的性质可得出BF=![]() AD,再结合三角形的中位线性质可得出EF=
AD,再结合三角形的中位线性质可得出EF=![]() CN,由线段间的关系即可证出结论;
CN,由线段间的关系即可证出结论;
(3)找出EN所扫过的图形为四边形DFCN.根据正方形以及等腰直角三角形的性质可得出BD∥CN,由此得出四边形DFCN为梯形,再由AB=1,可算出线段CF、DF、CN的长度,利用梯形的面积公式即可得出结论.
(1)①依题意补全图形,如图1所示.


②证明:连接CE,如图2所示.
∵四边形ABCD是正方形,
∴∠BCD=90°,AB=BC,
∴∠ACB=∠ACD=![]() ∠BCD=45°,
∠BCD=45°,
∵∠CMN=90°,CM=MN,
∴∠MCN=45°,
∴∠ACN=∠ACD+∠MCN=90°.
∵在Rt△ACN中,点E是AN中点,
∴AE=CE=![]() AN.
AN.
∵AE=CE,AB=CB,
∴点B,E在AC的垂直平分线上,
∴BE垂直平分AC,
∴BE⊥AC.
(2)BE=![]() AD+
AD+![]() CN.
CN.
证明:∵AB=BC,∠ABE=∠CBE,
∴AF=FC.
∵点E是AN中点,
∴AE=EN,
∴FE是△ACN的中位线.
∴FE=![]() CN.
CN.
∵BE⊥AC,
∴∠BFC=90°,
∴∠FBC+∠FCB=90°.
∵∠FCB=45°,
∴∠FBC=45°,
∴∠FCB=∠FBC,
∴BF=CF.
在Rt△BCF中,BF2+CF2=BC2,
∴BF=![]() BC.
BC.
∵四边形ABCD是正方形,
∴BC=AD,
∴BF=![]() AD.
AD.
∵BE=BF+FE,
∴BE=![]() AD+
AD+![]() CN.
CN.
(3)在点M沿着线段CD从点C运动到点D的过程中,线段EN所扫过的图形为四边形DFCN.

∵∠BDC=45°,∠DCN=45°,
∴BD∥CN,
∴四边形DFCN为梯形.
∵AB=1,
∴CF=DF=![]() BD=
BD=![]() ,CN=
,CN=![]() CD=
CD=![]() ,
,
∴S梯形DFCN=![]() (DF+CN)CF=
(DF+CN)CF=![]() (
(![]() +
+![]() )×
)×![]() =
=![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某店经销的甲型号手机今年的售价比去年每台降价500元.如果卖出相同数量的手机,那么去年销售额为8万元,今年销售额只有6万元.
(1)今年甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划购进乙型号手机销售,已知甲型号手机每台进价为1000元,乙型号手机每台进价为800元,预计用不多于1.84万元且不少于1.76万元的资金购进这两种手机共20台,请问有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
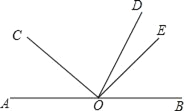
【题目】如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°.
(1)若∠AOC=48°,求∠DOE的度数.
(2)若∠AOC=α,则∠DOE= (用含α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究机构经过抽样调查,发现当地1500个老年人的养老模式主要有A,B,C,D,E五种,统计结果如图,那么下列说法不正确的是( )
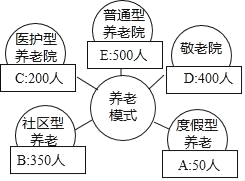
A. 选择A型养老的频率是![]()
B. 可以估计当地30000个老年人中有8000人选择C型养老
C. 样本容量是1500
D. 总体是当地1500个老年人的养老模式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动.
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com