
【题目】如图,在![]() 中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
(1)求证:AB=CE;
(2)若![]() ,则四边形ABEC是什么特殊四边形?请说明理由.
,则四边形ABEC是什么特殊四边形?请说明理由.

【答案】(1)证明见解析;(2)矩形,理由见解析.
【解析】
(1)根据AB//CD可知∠ABF=∠ECF,由BF=CF,∠AFB=∠CFE, 可证明△ABF≌△ECF.即可证明AB=CE.(2)根据∠AFC=2∠D 及外角性质可证明AF=BF进而证明AE=BC,即可证明四边形ABEC是平行四边形.
(1)∵F是BC的中点,
∴BF=CF.
∵在四边形![]() 中,AB//CD,
中,AB//CD,
∴∠ABF=∠ECF,
∵∠AFB=∠CFE,
∴△ABF≌△ECF,
∴AB=CE.
(2)四边形ABEC是矩形,理由如下:
∵△ABF≌△ECF,
∴EF=AF,
∵BF=CF,
∴四边形ABEC是平行四边形.
∴∠ABF=∠D,
∵∠AFC=2∠D,∠AFC=∠ABF+∠BAF,
∴∠ABF=∠BAF,
∴AF=BF,
∴AE=BC,
∴四边形ABEC是矩形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场代销甲、乙两种商品,其中甲种商品进价为120元/件,售价为130元/件,乙种商品进价为100元/件,售价为150元/件.
(1)若商场用36000元购进这两种商品若干,销售完后可获利润6000元,则该商场购进甲、乙两种商品各多少件?(列方程组解答)
(2)若商场购进这两种商品共100件,设购进甲种商品x件,两种商品销售后可获总利润为y元,请写出y与x的函数关系式(不要求写出自变量x的范围),并指出购进甲种商品件数x逐渐增加时,总利润y是增加还是减少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 图象
图象![]() 轴上方的部分沿
轴上方的部分沿![]() 轴翻折到
轴翻折到![]() 轴下方,图象的其余部分保持不变,翻折后的图象与原图象
轴下方,图象的其余部分保持不变,翻折后的图象与原图象![]() 轴下方的部分组成一个“
轴下方的部分组成一个“![]() ”形状的新图象,若直线
”形状的新图象,若直线![]() 与该新图象有两个公共点,则
与该新图象有两个公共点,则![]() 的取值范围为_____.
的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
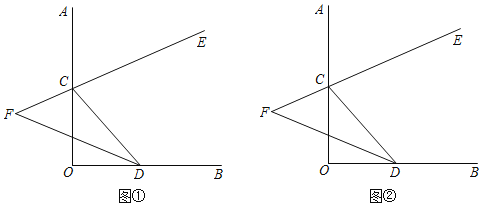
【题目】如图,∠AOB=90°,点C,D分别在射线OA,OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.
(1)当∠OCD=56°(如图①),试求∠F;
(2)当C,D在射线OA、OB上任意移动时(不与点O重合)(如图②),∠F的大小是否变化?若变化,请说明理由若不变化求出∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M为抛物线![]() 与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.
与x轴的焦点为A(-3,0),B(1,0),与y轴交于点C,连结AM,AC,点D为线段AM上一动点(不与A重合),以CD为斜边在CD上侧作等腰Rt△DEC,连结AE,OE.
(1)求抛物线的解析式及顶点M的坐标;
(2)求解AD:OE的值;
(3)当△OEC为直角三角形时,求AD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )

A. 7 B. 8 C. 7![]() D. 7
D. 7![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com