
【题目】如图,∠AOB=90°,点C,D分别在射线OA,OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.
(1)当∠OCD=56°(如图①),试求∠F;
(2)当C,D在射线OA、OB上任意移动时(不与点O重合)(如图②),∠F的大小是否变化?若变化,请说明理由若不变化求出∠F.
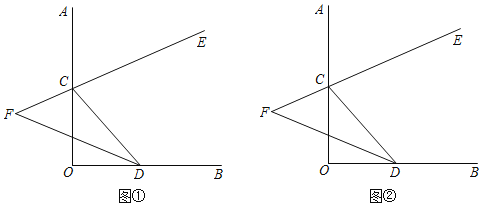
【答案】(1)∠F=45°;(2)不变,∠F=45°.
【解析】
(1)首先求出∠CDO=34°,∠ACD=124°,进而得到∠ECD=62°,∠CDF=17°,再根据三角形的外角等于与它不相邻的两内角之和,可求∠F=∠ECD﹣∠CDF;
(2)根据三角形外角的性质和角平分线定义求出∠ECD=![]() (90°+∠CDO),∠CDF=
(90°+∠CDO),∠CDF=![]() ∠CDO,然后根据三角形的外角等于与它不相邻的两内角之和,可求∠F=∠ECD﹣∠CDF.
∠CDO,然后根据三角形的外角等于与它不相邻的两内角之和,可求∠F=∠ECD﹣∠CDF.
(1)∵∠AOB=90°,∠OCD=56°,
∴∠CDO=34°,∠ACD=124°,
∵CE是∠ACD的平分线,DF是∠CDO的平分线,
∴∠ECD=62°,∠CDF=17°,
∵∠ECD=∠F+∠CDF,
∴∠F=∠ECD -∠CDF =45°;
(2)∠F不变,
∵∠ECD=![]() ∠ACD=
∠ACD=![]() (90°+∠CDO),
(90°+∠CDO),
∴∠ECD=45°+![]() ∠CDO,
∠CDO,
∵∠CDF=![]() ∠CDO,
∠CDO,
∴∠F=∠ECD﹣∠CDF,
=45°+![]() ∠CDO﹣
∠CDO﹣![]() ∠CDO,
∠CDO,
=45°.


科目:初中数学 来源: 题型:
【题目】(1)问题发现,
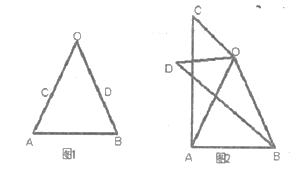
如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,将点
上一点,将点![]() 绕点
绕点![]() 顺时针旋转50°得到点
顺时针旋转50°得到点![]() ,则
,则![]() 与
与![]() 的数量关系是________________________。
的数量关系是________________________。
(2)类比探究
如图2,将(1)中的![]() 绕点
绕点![]() 在平面内旋转,(1)中的结论是否成立,并就图2的情形说明理由。
在平面内旋转,(1)中的结论是否成立,并就图2的情形说明理由。
(3)拓展延伸
![]() 绕点
绕点![]() 在平面旋转,当旋转到
在平面旋转,当旋转到![]() 时,请直接写出
时,请直接写出![]() 度数。
度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知命题“等腰三角形两腰上的高线长相等”
(1)请写出该命题的逆命题;
(2)判断(1)中命题的真假,并画出图形,补充已知,求证,及证明过程.
图形:
已知:在△ABC中,CD⊥AB,BE⊥AC,且______.
求证:______.
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,以
,以![]() 为直径在第一象限内作半圆,
为直径在第一象限内作半圆,![]() 为半圆上一点,连接
为半圆上一点,连接![]() 并延长至
并延长至![]() ,使
,使![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 于点
于点![]() ,已知
,已知![]() ,抛物线经过
,抛物线经过![]() 、
、![]() 、
、![]() 三点.
三点.

![]() ________°.
________°.
![]() 求抛物线的函数表达式.
求抛物线的函数表达式.
![]() 若
若![]() 为抛物线上位于第一象限内的一个动点,以
为抛物线上位于第一象限内的一个动点,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形面积记作
为顶点的四边形面积记作![]() ,则
,则![]() 取何值时,相应的点
取何值时,相应的点![]() 有且只有
有且只有![]() 个?
个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
(1)求证:AB=CE;
(2)若![]() ,则四边形ABEC是什么特殊四边形?请说明理由.
,则四边形ABEC是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,自行车成为人们喜爱的交通工具.某品牌共享自行车在温州的投放量自2017年起逐月增加,据统计,该品牌共享自行车1月份投放了640辆,3月份投放了1000辆.
(1)该品牌共享自行车前3个月的投放量的月平均增长率相同,则这三个月一共投放了多少辆自行车?
(2)考虑到增强客户体验,该品牌共享自行车准备投入3万元向自行车生产厂商定制了一批两种规格比较高档的自行车,之后投放到某高端写字楼区域.已知自行车生产厂商生产A型车的成本价为300元/辆,售价为500元/辆,生产B型车的成本价为700元/辆,售价为1000元/辆.根据指定要求,B型车的数量需超过12辆,且A型车的数量不少于B型车的2倍.自行车生产厂商应如何设计生产方案才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是经过∠BCA的顶点C的一条直线,CA=CB,E,F是直线CD上的两点,且∠BEC=∠CFA=α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图(a),若∠BCA=90°,α=90°,则BE________CF,EF________|BE-AF|(填“>”“<”或“=”);
②如图(b),若0°<∠BCA<180°,请添加一个关于α与∠BCA关系的条件________,使①中的两个结论仍然成立,并证明两个结论成立;
(2)如图(c),若直线CD经过∠BCA的外部,∠BCA=α,请写出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以![]() cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.
cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.
(1)当P异于A.C时,请说明PQ∥BC;
(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P与边BC分别有1个公共点和2个公共点?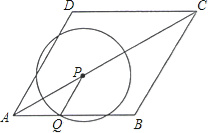
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com