
【题目】“低碳生活,绿色出行”,自行车成为人们喜爱的交通工具.某品牌共享自行车在温州的投放量自2017年起逐月增加,据统计,该品牌共享自行车1月份投放了640辆,3月份投放了1000辆.
(1)该品牌共享自行车前3个月的投放量的月平均增长率相同,则这三个月一共投放了多少辆自行车?
(2)考虑到增强客户体验,该品牌共享自行车准备投入3万元向自行车生产厂商定制了一批两种规格比较高档的自行车,之后投放到某高端写字楼区域.已知自行车生产厂商生产A型车的成本价为300元/辆,售价为500元/辆,生产B型车的成本价为700元/辆,售价为1000元/辆.根据指定要求,B型车的数量需超过12辆,且A型车的数量不少于B型车的2倍.自行车生产厂商应如何设计生产方案才能获得最大利润?最大利润是多少?
【答案】(1)这3个月一共投放了2440辆车.(2)生产A型车34辆,B型车13辆,生产商有最大利润为10700元.
【解析】
(1)设前3个月的月平均增长率为x,根据题意列出方程即可求出答案.(2)设生产B型车x辆,根据题意列不等式组,解不等式组得x为13、14、15、根据利润(W)的解析式可知W随x的增大而减小,所以x为13时利润最大,通过解析式求出利润即可.
(1)设前3个月的月平均增长率为x,根据题意得:![]()
解得![]() (舍去)
(舍去)![]()
![]() (辆)
(辆)
答:这3个月一共投放了2440辆车.
(2)①设生产B型车x辆,则生产A型车![]() 辆,根据题意,
辆,根据题意,
得
解得![]() ,
,
∵x为正整数,∴x=13,14,15
设生产产商的利润为W,由题意得
W=(500-300)(60-2x)+(1000-700)x=12000-100x
∵k=-100<0,∴W随x的增大而减小
∴当x=13时,![]() . ∴
. ∴![]() (辆)
(辆)
答:生产A型车34辆,B型车13辆,生产商有最大利润为10700元.


科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,点C,D分别在射线OA,OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.
(1)当∠OCD=56°(如图①),试求∠F;
(2)当C,D在射线OA、OB上任意移动时(不与点O重合)(如图②),∠F的大小是否变化?若变化,请说明理由若不变化求出∠F.
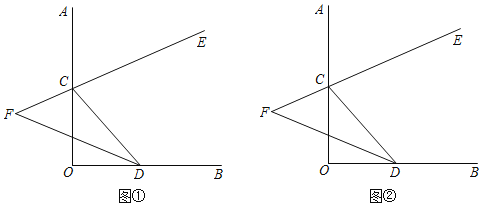
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在△ABC中,∠BAC=90,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D.E证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D. A.E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,请问结论DE=BD+CE是否成立,若成立,请你给证明:若不存在,请说明理由。
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,D. A.E三点都在直线m上,且∠BDA=∠AEC=∠BAC,只出现m与BC的延长线交于点F,若BD=5,DE=7,EF=2CE,求△ABD与△ABF的面积之比。
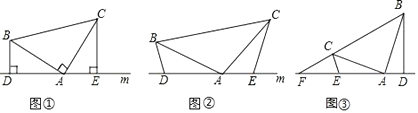
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形网格上有6个三角形:①△ABC;②△BCD;③△BDE;④△BFG;⑤△FGH;⑥△EFK.其中②~⑥中与①相似的是( )

A. ②③④ B. ③④⑤ C. ④⑤⑥ D. ②③⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是正方形ABCD的对角线AC上的两点,且AE=CF.
(1)求证:四边形BEDF是菱形;
(2)若正方形ABCD的边长为4,AE=![]() ,求菱形BEDF的面积.
,求菱形BEDF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
问题:已知方程x2+x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x,所以x=![]() ,把x=
,把x=![]() ,代入已知方程,
,代入已知方程,
得(![]() )2 +
)2 +![]() ﹣1=0.
﹣1=0.
化简,得y2+2y﹣4=0,
故所求方程为y2+2y﹣4=0
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式):
(1)已知方程x2+2x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为 ;
(2)已知关于x的一元二次方程ax2+bx+c=0(a≠0)有两个不等于零的实数根,求一个一元二次方程,使它的根分别是已知方程根的倒数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com