
����Ŀ���Ķ����в��ϣ�
���⣺��֪����x2+x��1=0����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸���2����
�⣺�����̵ĸ�Ϊy����y=2x������x=![]() ����x=
����x=![]() ��������֪���̣�
��������֪���̣�
�ã�![]() ��2 +
��2 +![]() ��1=0��
��1=0��
����y2+2y��4=0��
������Ϊy2+2y��4=0
�������÷��̸��Ĵ������·��̵ķ��������dz�Ϊ������������
�����Ķ������ṩ���������������·��̣�Ҫ�����̻�Ϊһ����ʽ����
��1����֪����x2+2x��1=0����һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸����෴����������Ϊ ��
��2����֪����x��һԪ���η���ax2+bx+c=0��a��0�����������������ʵ��������һ��һԪ���η��̣�ʹ���ĸ��ֱ�����֪���̸��ĵ�����
���𰸡���1��y2��2y��1=0����2������Ϊa+by+cy2=0�� c��0����
�����������������(1)����Ϊ�෴�����������ĺ�Ϊԭ�����͵��෴���������䣬�Ӷ��ó����̣�(2)�������̵ĸ�Ϊy����y=![]() (x��0),����x=
(x��0),����x=![]() (y��0)��Ȼ��x=
(y��0)��Ȼ��x=![]() ���뷽�̣��Ӷ��ó�����ķ���.
���뷽�̣��Ӷ��ó�����ķ���.
���������(1)�� y2-2y-1=0
(2)�������̵ĸ�Ϊy����y=![]() (x��0),����x=
(x��0),����x=![]() (y��0)
(y��0)
��x=![]() ���뷽��ax2+bx+c=0, ��a (
���뷽��ax2+bx+c=0, ��a (![]() )2+b��
)2+b��![]() ��+c=0
��+c=0
ȥ��ĸ���� a+by+cy2=0
��c=0����ax2+bx="0" ,���ǣ�����ax2+bx+c=0��һ����Ϊ0����������
�� c��0����������a+by+cy2=0 ( c��0) .



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ʾ��AC=CD����B=��E=90�㣬AC��CD������ȷ�Ľ����ǣ�������
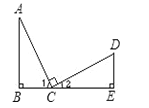
A. ��1=��2 B. ��A =��2 C. ��ABC�ա�CED D. ��A���D��Ϊ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����䷽����һԪ���η���x2+4x��3=0ʱ��ԭ���̿ɱ���Ϊ�� ��
A.��x+2��2=1
B.��x+2��2=7
C.��x+2��2=13
D.��x+2��2=19
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������xy��2��4x2y3����������Ӧ��ĵ���ʽ�ǣ�������
A. ��4yB. 4yC. 4xyD. ��2xy
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A.2a+3b��5abB.��a+b��2��a2+b2
C.a2a3��a6D.5a��2a��3a
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����100ԪǮȥ����ʼDZ��ֱʹ�15������֪ÿ���ʼDZ�5Ԫ��ÿ֧�ֱ�7Ԫ��С���������_____֧�ֱʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com