
【题目】如图的三角形纸片中,AB=AC,BC=12cm,∠C=30°,折叠这个三角形,使点B落在AC的中点D处,折痕为EF,那么BF的长为cm. 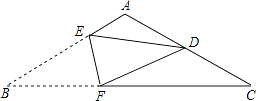
【答案】![]()
【解析】解:过D作DH⊥BC,过点A作AN⊥BC于点N, 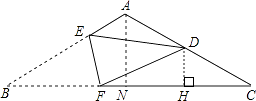
∵AB=AC,
∴∠B=∠C=30°,
根据折叠可得:DF=BF,∠EDF=∠B=30°,
∵AB=AC,BC=12cm,
∴BN=NC=6cm,
∵点B落在AC的中点D处,AN∥DH,
∴NH=HC=3cm,
∴DH=3tan30°= ![]() (cm),
(cm),
设BF=DF=xcm,则FH=12﹣x﹣3=9﹣x(cm),
故在Rt△DFC中,DF2=DH2+FH2 ,
故x2=( ![]() )2+(9﹣x)2 ,
)2+(9﹣x)2 ,
解得:x= ![]() ,
,
即BF的长为: ![]() cm.
cm.
故答案为: ![]() .
.
首先过D作DH⊥BC,过点A作AN⊥BC于点N,根据题意结合等腰三角形的性质进而得出CN的长,再利用锐角三角函数关系以及勾股定理得出答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某学校组织学生到富阳春游,需要乘船到达目的地,有大小两种船,705班共有学生51人,如果租用大船4艘,小船1艘,则有3位同学没有座位;如果租用大船3艘,小船3艘,则有3个座位空余。
(1)问大小船每艘各坐几人?
(2)如果大船收费标准为30元/艘,小船收费标准为25元/艘,请直接写出你的设计方案使得租船费用最低,并计算最低费用。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直径坐标系中,抛物线y=ax2+bx﹣2与x轴交于点A(﹣3,0).B(1,0),与y轴交于点C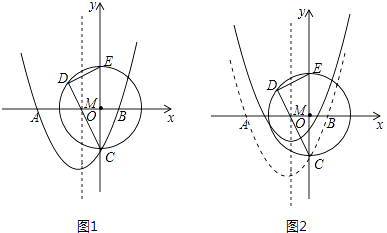
(1)直接写出抛物线的函数解析式;
(2)以OC为半径的⊙O与y轴的正半轴交于点E,若弦CD过AB的中点M,试求出DC的长;
(3)将抛物线向上平移 ![]() 个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
个单位长度(如图2)若动点P(x,y)在平移后的抛物线上,且点P在第三象限,请求出△PDE的面积关于x的函数关系式,并写出△PDE面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象经过点A(0,2)和点B(-a,3),且点B在正比例函数y=-3x的图象上.
(1)求a的值;
(2)求一次函数的解析式并画出它的图象;
(3)若P(m,y1),Q(m-1,y2)是这个一次函数图象上的两点,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设资源节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)小张家今年2月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少元/千瓦时;
(2)若6月份小张家预计用电130千瓦时,请预算小张家6月份应上缴的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAE,交BF于C. 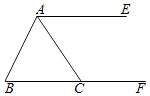
(1)尺规作图:过点B作AC的垂线,交AC于O,交AE于D,(保留作图痕迹,不写作法);
(2)在(1)的图形中,找出两条相等的线段,并予以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校需购买一批课桌椅供学生使用,已知A型课桌椅230元/套,B型课桌椅200元/套.
(1)该校购买了A,B型课桌椅共250套,付款53000元,求A,B型课桌椅各买了多少套?
(2)因学生人数增加,该校需再购买100套A,B型课桌椅,现只有资金22000元,最多能购买A型课桌椅多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个两位数,十位数字是a,十位数字比个位数字小2,这个两位数是( )
A.a(a+2)B.10a(a+2)C.10a+(a+2)D.10a+(a﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com