

分析 (1)根据题意和三角形全等的判定证明△CAO≌△DBO,根据全等三角形的性质得到答案;
(2)证明△QOC≌△POD,即可得到CQ=DP;
(3)根据△QOC≌△POD,求出PD的长,即可得到CQ的长.
解答 解:(1)∵点O是AB的中点,
∴AO=BO,
又∵BD=AO,
∴BD=BO,
∴∠DOB=∠BDO=45°,
又∵AC=AO,
∴AC=BD,
在△CAO和△DBO中,
$\left\{\begin{array}{l}{AC=BD}\\{∠A=∠B}\\{AO=BO}\end{array}\right.$,
∴△CAO≌△DBO,
∴OC=OD,∠COA=∠BOD=45°,
∴∠COD=α=90°;
(2)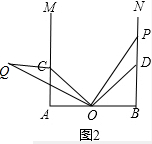 如图2,
如图2,
∵∠COD=∠POQ=90°,
∴∠QOC=∠POD,
在△QOC和△POD中,
$\left\{\begin{array}{l}{QO=PO}\\{∠QOC=∠POD}\\{OC=OD}\end{array}\right.$,
∴△QOC≌△POD,
∴CQ=DP;
(3)∵OD=OC=$\sqrt{2}a$,△BOD是等腰直角三角形,
∴BD=OB=a,
∵∠OPD=∠OQC=30°,
∴BP=$\sqrt{3}$a,
则PD=$\sqrt{3}$a-a,
∴CQ=PD=($\sqrt{3}$-1)a.
点评 本题考查的是旋转变换的性质、全等三角形的判定和性质,理解旋转方向、旋转角和旋转中心的概念、掌握全等三角形的判定定理和性质定理是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
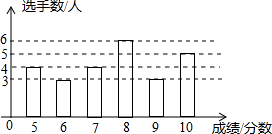
| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
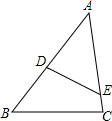 如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=4cm,△ADE的面积是4cm2,四边形BCED的面积是5cm2,那么AB的长是6cm.
如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=4cm,△ADE的面积是4cm2,四边形BCED的面积是5cm2,那么AB的长是6cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
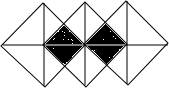 如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )
如图,如果可以在三个完全相同的正方形拼成的图案中随意取点,那么这个点取在阴影部分的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
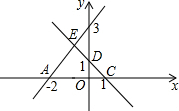 如图,直线AB分别与x轴、y轴交于点A(-2,0),B(0,3).直线CD分别与x轴、y轴交于点C(1,0),D(0,1),与直线AB交于点E.求点E的坐标.
如图,直线AB分别与x轴、y轴交于点A(-2,0),B(0,3).直线CD分别与x轴、y轴交于点C(1,0),D(0,1),与直线AB交于点E.求点E的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com