
【题目】如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠CAD.
(1)求证:直线MN是⊙O的切线;
(2)若CD=3,∠CAD=30°,求⊙O的半径.
【答案】
(1)
证明:连接OC,
因为OA=OC,
所以∠BAC=∠ACO.
因为AC平分∠BAD,
所以∠BAC=∠CAD,
故∠ACO=∠CAD.
所以OC∥AD,
又已知AD丄MN,
所以OC丄MN,
所以,直线MN是⊙O的切线
(2)
解:已知AB是⊙O的直径,则∠ACB=90°,
又AD丄MN,
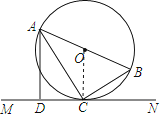
则∠ADC=90°.
因为CD=3,∠CAD=30°,
所以AD=3 ![]() ,AB=6
,AB=6
在Rt△ABC和Rt△ACD中,∠BAC=∠CAD,
所以Rt△ABC∽Rt△ACD,
则 ![]() ,
,
则AB=4 ![]() ,
,
所以⊙O的半径为2 ![]()
【解析】(1)连接OC,推出AD∥OC,推出OC⊥MN,根据切线的判定推出即可;(2)求出AD、AC长,证△ADC∽△ACB,得出比例式,代入求出AB长即可.本题考查了切线的判定,等腰三角形的判定和性质,平行线性质,相似三角形的性质和判定的应用,主要考查学生运用定理进行推理和计算的能力.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对切线的判定定理的理解,了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点![]() 点D不与B,C重合
点D不与B,C重合![]() 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
![]() 如图1,求证:
如图1,求证:![]() ≌
≌![]() ;
;
![]() 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;
![]() 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问![]() 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC与BD交于O,下列条件中不一定能判定这个四边形是平行四边形的是( )

A. AB=DC,AD=BC B. AD∥BC,AB∥DC
C. OA=OC,OB=OD D. AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知∠DAB=∠DCB,AF平分∠DAB,CE平分∠DCB,∠FCE=∠CEB,试说明:AF∥CE。

解:(1)因为∠DAB=∠DCB( ),
又AF平分∠DAB,
所以_____=![]() ∠DAB( ),
∠DAB( ),
又因为CE平分∠DCB,
所以∠FCE=_____( ),
所以∠FAE=∠FCE。
因为∠FCE=∠CEB,
所以______=________
所以AF∥CE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校九年级学生举行朗诵比赛,全年级学生都参加,学校对表现优异的学生进行表彰,设置一、二、三等奖各进步奖共四个奖项,赛后将九年级(1)班的获奖情况绘制成如图所示的两幅不完整的统计图,请根据图中的信息,解答下列问题: 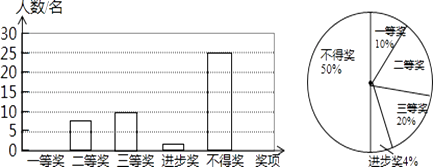
(1)九年级(1)班共有名学生;
(2)将条形图补充完整:在扇形统计图中,“二等奖”对应的扇形的圆心角度数是;
(3)如果该九年级共有1250名学生,请估计荣获一、二、三等奖的学生共有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解2016年初中毕业生毕业后的去向,某县教育局对部分初三学生进行了抽样调查,就初三学生的四种去向(A,读普通高中;B,读职业高中; C,直接进入社会就业; D,其它)进行数据统计,并绘制了两幅不完整的统计图(a)、(b).请根据图中信息解答下列问题: 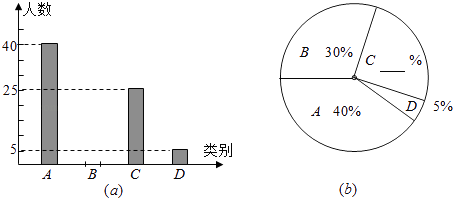
(1)该县共调查了多少名初中毕业生?
(2)通过计算,将两幅统计图中不完整的部分补充完整;
(3)若该县2016年初三毕业生共有4500人,请估计该县今年的初三毕业生中准备读普通高中的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E,F分别是线段BC,AD的中点,AB=2,AD=4,动点P沿EC,CD,DF的路线由点E运动到点F,则△PAB的面积s是动点P运动的路径总长x的函数,这个函数的大致图象可能是
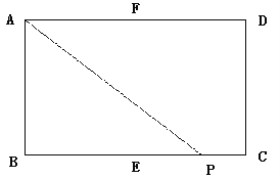
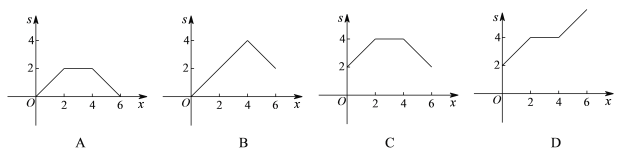
A. A B. B C. C D. D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com