
����Ŀ��ij������7��30��С���ڼ�ͨ���εδ�������ǰ������վ��˵�������8��30�Ķ���������������ʻʱ��ΪtСʱ����ʻ�ٶ�Ϊvǧ��/Сʱ��������ʻ�ٶȲ�����60ǧ��/Сʱ�������ݾ��飬v��t��һ���Ӧֵ���±���
V��ǧ��/Сʱ�� | 20 | 30 | 40 | 50 | 60 |
T��Сʱ�� | 0.6 | 0.4 | 0.3 | 0.25 | 0.2 |
��1�����ݱ��е�������㣬���ƽ���ٶ�v��ǧ��/Сʱ��������ʻʱ��t��Сʱ���ĺ�������ʽ��
��2����С���ӿ�ʼ���ϳ�����10���ӣ�С�����ڶ�������ǰ��Сʱ���ﶯ��վ����������ƽ���ٶ�Ϊ32ǧ��/Сʱ��С���ܷ���Ԥ����ʱ���ڵ��ﶯ��վ����˵�����ɣ�
��3�����������ﶯ��վ����ʻʱ��t����0.3��t��0.5����ƽ���ٶ�v��ȡֵ��Χ��

���𰸡���1��v=![]() ����2����������ƽ���ٶ�Ϊ32ǧ��/Сʱ��С��������Ԥ����ʱ���ڵ��ﶯ��վ����3��ƽ���ٶ�v��ȡֵ��Χ��24��v��40
����2����������ƽ���ٶ�Ϊ32ǧ��/Сʱ��С��������Ԥ����ʱ���ڵ��ﶯ��վ����3��ƽ���ٶ�v��ȡֵ��Χ��24��v��40
��������
��1�����ݱ��������ݣ���֪v��t�ķ�������������v=![]() �����ô���ϵ�������k���ɣ�
�����ô���ϵ�������k���ɣ�
��2������ʱ��t=![]() Сʱ������ٶȣ������жϣ�
Сʱ������ٶȣ������жϣ�
��3�������Ա�����ȡֵ��Χ���������ֵ��ȡֵ��Χ���ɣ�
��1�����ݱ��������ݣ���֪v=![]() ��
��
��v=20ʱ��t=0.6��
��k=20��0.6=12��
��v=![]() ��t��0.2����
��t��0.2����
��2����1��![]() -
-![]() =
=![]() ��
��
��t=![]() ʱ��v=
ʱ��v=![]() =36��32��
=36��32��
����������ƽ���ٶ�Ϊ32ǧ��/Сʱ��С��������Ԥ����ʱ���ڵ��ﶯ��վ��
��3����0.3��t��0.5��
��24��v��40��
��ƽ���ٶ�v��ȡֵ��Χ��24��v��40��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������ABC�ĵ�Ϊ30������BCΪֱ������O��ױ�AB���ڵ�D����D��DE��AC������ΪE��
(1)֤����DEΪ��O�����ߣ�
(2)��BC=4������Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
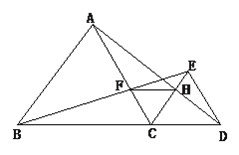
����Ŀ����ͼ����֪��B��C��D��ͬһ��ֱ���ϣ���ABC����CDE���ǵȱ�������.BE��AC��F��AD��CE��H��
����֤����BCE�ա�ACD��
����֤��CF=CH��
���ж���CFH����״��˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
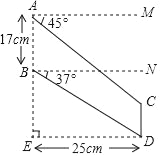
����Ŀ����C919�����Ϳͻ��ɳɹ���������ͬѧ�ǶԺ��տƼ�����Ȥ����ͼ��ijУ��ģ��ȤС���õ�һ�����ݲ������ĺ�ģ�ɻ�����ͼֽ��ͼ��AB��CD��AM��BN��ED��AE��DE�������ͼ�����ݣ�����߶�BE��CD�ij�����sin37���0.60��cos37���0.80��tan37���0.75���������С�����һλ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=mx+n�뷴��������y=![]() ������mn��0��m��n��Ϊ������������ͬһ����ϵ�е�ͼ������ǣ�������
������mn��0��m��n��Ϊ������������ͬһ����ϵ�е�ͼ������ǣ�������
A.  B.
B. 
C. 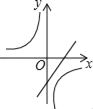 D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��BC��DC��BC��E��BC��һ�㣬ʹ��AE��DE��
��1����֤����ABE�ס�ECD��
��2����AB=4��AE=BC=5����CD�ij���
��3������AED�ס�ECDʱ����д���߶�AD��AB��CD֮��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AC��CB��O��AB���е㣬CA���O�����ڵ�E��CO����O�ڵ�D
��1����֤��CB�ǡ�O�����ߣ�
��2������ACB��80�㣬��P�ǡ�O��һ�����㣨����D��E�����غϣ������DPE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ֱ��y1��x+1��ƽ��ֱ������ϵxOy�У�

��1����ƽ��ֱ������ϵxOy�л���y2����2x+4��ͼ��
��2����y1��y2�Ľ������ꣻ
��3������ͼ��ֱ��д����y1��y2ʱ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵ�У���M����ԭ��O��0��0������A��![]() ��0�����B��0����1������D���ӻ�OA�ϣ�����BD��x���ڵ�C���ҡ�COD����CBO��
��0�����B��0����1������D���ӻ�OA�ϣ�����BD��x���ڵ�C���ҡ�COD����CBO��
��1����ֱ��д����M��ֱ��������֤BDƽ�֡�ABO��
��2�����߶�BD���ӳ�����Ѱ��һ��E��ʹ��ֱ��AEǡ������M���У����ʱ��E�����꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com