练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知：如图，直线y1＝x+1在平面直角坐标系xOy中．

    （1）在平面直角坐标系xOy中画出y2＝﹣2x+4的图象；

    （2）求y1与y2的交点坐标；

    （3）根据图象直接写出当y1≥y2时，x的取值范围．

    【答案】（1）y2＝﹣2x+4的图象如图所示，见解析；（2）y1与y2的交点坐标为（1，2）；（3）x的取值范围是x≥1．

    【解析】

    （1）依据函数解析式即可画出y2=-2x+4的图象；
    （2）解方程组可得y1与y2的交点坐标；
    （3）依据函数图象以及交点坐标即可得到当y1≥y2时，x的取值范围．

    （1）y2＝﹣2x+4的图象如图所示：

    （2）解方程组

    ，可得
    ，
    ∴y1与y2的交点坐标为（1，2）；
    （3）当y1≥y2时，x的取值范围是x≥1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，点B的坐标为（4，2），直线交AB，BC分别于点M，N，反比例函数的图象经过点M，N．

    （1）求反比例函数的解析式；

    （2）若点P在y轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某天上午7：30，小芳在家通过滴滴打车软件打车前往动车站搭乘当天上午8：30的动车．记汽车的行驶时间为t小时，行驶速度为v千米/小时（汽车行驶速度不超过60千米/小时）．根据经验，v，t的一组对应值如下表：

    V（千米/小时）

    20

    30

    40

    50

    60

    T（小时）

    0.6

    0.4

    0.3

    0.25

    0.2

    （1）根据表中的数据描点，求出平均速度v（千米/小时）关于行驶时间t（小时）的函数表达式；

    （2）若小芳从开始打车到上车用了10分钟，小芳想在动车出发前半小时到达动车站，若汽车的平均速度为32千米/小时，小芳能否在预定的时间内到达动车站？请说明理由；

    （3）若汽车到达动车站的行驶时间t满足0.3＜t＜0.5，求平均速度v的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，BC＝AC＝6，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．

    （1）求证：点D是AB的中点；

    （2）求点O到直线DE的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】《九章算术》是中国传统数学重要的著作，奠定了中国传统数学的基本框架．《九章算术》中记

    载：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，间径几何？”（如图①）

    阅读完这段文字后，小智画出了一个圆柱截面示意图（如图②），其中BO⊥CD于点A，求间径就是要求⊙O的直径．再次阅读后，发现AB=______寸，CD=____寸（一尺等于十寸），通过运用有关知识即可解决这个问题．请你补全题目条件，并帮助小智求出⊙O的直径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直线l1：y＝﹣2x+5与y轴交于点B，直线l2：y＝kx+b与x轴交于点D（1，0），与y轴交于点C，两直线交于点A（2，1）．

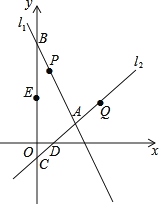
    （1）求直线l2的函数解析式．

    （2）求两直线与y轴围成的三角形的面积．

    （3）点P为l1上一动点，点Q为l2上一动点，点E（0，2），若以BE为一边，且以点B，E，P，Q为顶点的四边形为平行四边形，直接写出点Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在笔直的铁路上A、B两点相距25km，C、D为两村庄，DA=10km，CB=15km，DA⊥AB于A，CB⊥AB于B，现要在AB上建一个中转站E，使得C、D两村到E站的距离相等．求E应建在距A多远处？

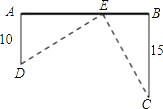
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系．

    （1）求水柱所在抛物线（第一象限部分）的函数表达式；

    （2）王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？

    （3）经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：由火柴棒拼出的一列图形，第个图形是由个等边三角形拼成的，通过观察，分析发现：第8个图形中平行四边形的个数（ ）．

    A.16B.18C.20D.22

    查看答案和解析>>

    同步练习册答案