
分析 因为1+2+1=4=22,1+2+3+2+1=9=32,1+2+3+4+3+2+1=16=42,1+2+3+4+5+4+3+2+1=25=52,…由此得出1+2+3+…+n+…+3+2+1=n2;据此解答.
解答 解:∵1+2+1=4=22,
1+2+3+2+1=9=32,
1+2+3+4+3+2+1=16=42,
1+2+3+4+5+4+3+2+1=25=52,
…
∴1+2+3+…+n+…+3+2+1=n2;
∴1+2+3+4+…+2004+2005+2004+…+4+3+2+1=20052=4020025.
故答案为:4,9,16,25,4020025.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.


科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x=0\\ y=6\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=\frac{1}{2}\\ y=5\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=-2\\ y=-10\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=3\\ y=0\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
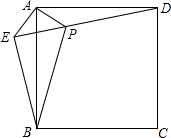 如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=2.
如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com