
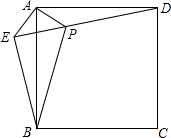
 如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=2.
如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=2.分析 (1)首先利用已知条件根据边角边可以证明△APD≌△AEB;
(2)①利用全等三角形的性质和对顶角相等即可解答;
②由△APD≌△AEB,可知S△APD+S△APB=S△AEB+S△APB,然后利用已知条件计算即可判定;
(3)由(1)可得∠BEP=90°,故BE不垂直于AE过点B作BM⊥AE延长线于F,由①得∠AEB=135°所以∠EFB=45°,所以△EFB是等腰Rt△,故B到直线AE距离为BF=$\sqrt{2}$;
(4)根据BF=EF=1,AF=EF+AE=1+1=2,再利用勾股定理解答即可.
解答 解:(1)在△APD与△AEB中,
$\left\{\begin{array}{l}{AD=AB}\\{∠PAP=∠BAE}\\{AP=AE}\end{array}\right.$
∴△APD≌△AEB(SAS),
故答案为:△AEB;
(2)①因为△APD≌△AEB,所以∠ADP=∠ABE,∠DOA=∠BOE,
∵∠ADP+∠DOA=90°,
∴∠ABE+∠BOE=90°,
∴∠DEB=90°,
∴AB⊥DE;
所以①正确;
②由△APD≌△AEB,
∵AE=AP=1,
∴PE=$\sqrt{2}$,在Rt△PBE中,BE=$\sqrt{{2}^{2}-(\sqrt{2})^{2}}=\sqrt{2}$
∴PD=BE=$\sqrt{2}$,
∴S△APD+S△APB=S△APE+S△BPE=$\frac{1}{2}×1×1+\frac{1}{2}×\sqrt{2}×\sqrt{2}=\frac{3}{2}$,所以②正确;
故答案为:①②;
(3)由△APD≌△AEB得,∠AEP=∠APE=45°,从而∠APD=∠AEB=135°,
所以∠BEP=90°,
过B作BF⊥AE,交AE的延长线于F,则BF的长是点B到直线AE的距离,如图1: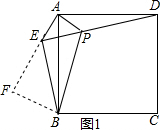
在△AEP中,由勾股定理得PE=$\sqrt{2}$,
在△BEP中,PB=2,PE=$\sqrt{2}$,由勾股定理得:BE=$\sqrt{{2}^{2}-(\sqrt{2})^{2}}=\sqrt{2}$,
∵∠PAE=∠PEB=∠EFB=90°,AE=AP,
∴∠AEP=45°,
∴∠BEF=180°-45°-90°=45°,
∴∠EBF=45°,
∴EF=BF=1,
∴点B到直线AE的距离为1,
故答案为:1;
(4)∵BF=EF=1,AF=EF+AE=1+1=2
在Rt△ABF中,S正方形ABCD=AB2=22+1=5.
点评 此题分别考查了正方形的性质、全等三角形的性质与判定、三角形的面积及勾股定理,综合性比较强,解题时要求熟练掌握相关的基础知识才能很好解决问题.


科目:初中数学 来源: 题型:解答题
| 星 期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 水位记录 | +2.40 | +0.60 | -4.00 | -1.60 | +3.50 | +2.00 | -1.50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
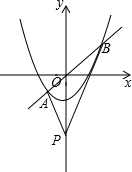 在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y=$\frac{1}{3}$x2-2交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),连结PA、PB,有以下说法:
在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线y=$\frac{1}{3}$x2-2交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),连结PA、PB,有以下说法:| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com