
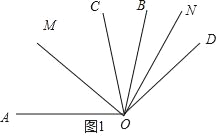
����Ŀ����ͼ����AOB��������COD����������������OC��OB�غϣ�OD�ڡ�AOB�⣬����OM��ON�ֱ��ǡ�AOC����BOD�Ľ�ƽ���ߣ�
��1����������100��������60�������MON���ڶ��٣�
���ڢٵ������¡�COD�Ƶ�O��ʱ����תn����0��n��100����n��60��ʱ�����MON�Ķ�����
��2��ֱ��д����COD�Ƶ�O��ʱ����תn����0��n��360��ʱ��MON��ֵ���ú���������ʽ�ӱ�ʾ����

���𰸡���1���١�MON��80�㣻�ڡ�MON��80�㣻��2����MON��![]() ����+������180�㩁
����+������180�㩁![]() ����+������
����+������
��������
��1���ٸ��ݽ�ƽ���ߵĶ��������BOM�͡�CON�Ķ�����Ȼ����Ӽ��ɵó��𰸣�
�ڸ�����ת�����ʿ�֪��BOC=n�㣬����������������ۣ���ͼ1����BOD��60�㩁n�㣬��AOC��100����n�������ݽ�ƽ���ߵĶ���ó���COM�͡�BON�Ķ�����Ȼ����ݡ�MON����COM+��COB+��BON���м��㼴�ɵó����ۣ���ͼ2����BOD��n����60������AOC��100����n�������ݽ�ƽ���ߵĶ���ó���COM�͡�BON�Ķ�����Ȼ����ݡ�MON����COM+��COD+��BON���м��㼴�ɵó����ۣ�
��2�����ݢ١��ڵĽ���˼·���ɵõ����ۣ�
��1���١�OM��ON�ֱ��ǡ�AOC����BOD�Ľ�ƽ���ߣ�
���BOM��![]() ��AOB����BON��
��AOB����BON��![]() ��BOD��
��BOD��
���MON��![]() ����AOB+��BOD����
����AOB+��BOD����
�֡ߡ�AOB��100������COD��60����
���MON��![]() ����AOB+��BOD����
����AOB+��BOD����![]() ����100��+60������80����
����100��+60������80����
����ͼ1���ߡ�COD�Ƶ�O��ʱ����תn����
���BOC��n����
���BOD��60����n������AOC��100����n����
��OM��ON�ֱ��ǡ�AOC����BOD�Ľ�ƽ���ߣ�
���COM��![]() ��AOC��50����
��AOC��50����![]() n������BON��
n������BON��![]() ��BOD��30����
��BOD��30����![]() n����
n����
���MON����COM+��COB+��BON��80����
��ͼ2���ߡ�COD�Ƶ�O��ʱ����תn����
���BOC��n����
���BOD��n����60������AOC��100����n����
��OM��ON�ֱ��ǡ�AOC����BOD�Ľ�ƽ���ߣ�
���COM��![]() ��AOC��50����
��AOC��50����![]() n������DON��
n������DON��![]() ��BOD��
��BOD��![]() n����30����
n����30����
���MON����COM+��COD+��DON��80����
��2����OMΪ��AOD��ƽ���ߣ�ONΪ��BOC��ƽ���ߣ���AOB��������COD������
���MON��![]() ����+������180����
����+������180����![]() ����+������
����+������


 ����5��2���ϵ�д�
����5��2���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı���ABCD�У���E��AD���ϣ�����BE��CE��EBƽ�֡�AEC .
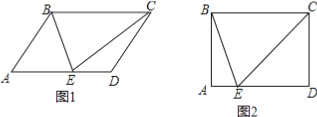
��1����ͼ1���жϡ�BCE����״����˵�����ɣ�
��2����ͼ2������A=90�㣬BC=5��AE=1�����߶�BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ⱳ������֪:l ��m��n��k��ƽ����l��m��m��n��n��k֮��ľ���ֱ�Ϊd1��d2��d3 �� ��d1 =d3 = 1��d2 = 2 �����ǰ��ĸ�����ֱ���l��m��n��k������ƽ�����ϵ��ı��γ�Ϊ�������ı��Ρ���
��1����̽��1����ͼ1��������ABCDΪ�������ı��Ρ���BE![]() L�ڵ�E,BE�ķ����ӳ��߽�ֱ��k�ڵ�F�� ��������ABCD�ı߳���
L�ڵ�E,BE�ķ����ӳ��߽�ֱ��k�ڵ�F�� ��������ABCD�ı߳���
��2����̽��2������ABCDΪ�������ı��Ρ����䳤 ���� = 2 ��1 �������ABCD�Ŀ�
��3����̽��3����ͼ2������ABCDΪ�������ı��Ρ��ҡ�ADC=60�㣬��AEF�ǵȱ������Σ� ![]() �ڵ�E�� ��AFD=90�㣬ֱ��DF�ֱ�ֱ��l��k�ڵ�G��M�� ��֤��EC=DF��
�ڵ�E�� ��AFD=90�㣬ֱ��DF�ֱ�ֱ��l��k�ڵ�G��M�� ��֤��EC=DF��
��4������ չ����ͼ3��l ��k���ȱ�������ABC�Ķ���A��B�ֱ�����ֱ��l��k�ϣ� ![]() �ڵ�B����AB=4 ����ACD=90�㣬ֱ��CD�ֱ�ֱ��l��k�ڵ�G��M����D��E�ֱ����߶�GM��BM�ϵĶ��㣬��ʼ�ձ���AD=AE��
�ڵ�B����AB=4 ����ACD=90�㣬ֱ��CD�ֱ�ֱ��l��k�ڵ�G��M����D��E�ֱ����߶�GM��BM�ϵĶ��㣬��ʼ�ձ���AD=AE�� ![]() �ڵ�H��
�ڵ�H��
���룺DH��ʲô��Χ�ڣ�BC��DE��ֱ��д�����ۡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס����������������ֱ���A��B����ͬʱ������������С��׳���ʻ85ǧ�����ҳ�������Ȼ�����ǰ������������Է��ij�����Ⱥ�30����������ԭ·���ء����׳���ʻ65ǧ�������ҳ���������A��B���صľ��롣
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ϵ�У�![]() �Ķ������궼��������ϣ����е�C������Ϊ
�Ķ������궼��������ϣ����е�C������Ϊ![]() ��
��

��1�����A��B������![]()
��2����![]() ������ƽ��2����λ���ȣ�������ƽ��1����λ���ȣ��õ�
������ƽ��2����λ���ȣ�������ƽ��1����λ���ȣ��õ�![]() ����
����![]() ��������������ֱ���
��������������ֱ���![]()
��3������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������ҳ���ͬ������ͬһ��ɲ��ʽ��������1����������1����������1ƿ��������Һ��ɣ���������Һ��Ϊ��Ʒ�ɵ�������1ƿ��������Һ���ۼ���1����������![]() ����֪��������Һ��������Ϊ20%��������������������Ϊ25%���Ű��̴Ӽ׳�������1��������������������������4ƿ��������Һ�����д��й�����10Ԫ��
����֪��������Һ��������Ϊ20%��������������������Ϊ25%���Ű��̴Ӽ׳�������1��������������������������4ƿ��������Һ�����д��й�����10Ԫ��
��1����1����������1ƿ��������Һ���ۼۣ�
��2��Ϊ�˴ٽ��ÿ������������ۣ��׳��д�8.5�����ۣ����ҳ��в��õ����۷����ǹ˿�ÿ��1����������1ƿ��������Һ������δ����ڼ䣬�׳�������2000�������������ҳ����������������ϻ�õ������ڼ׳��е�1.2�������ҳ����������۶�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У���BAD��ƽ����AE��DC�ڵ�E.
(1)��֤��AD��DE��
(2)��AB��CB��3��2��CE��5 cm����ABCD���ܳ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
�л����㴫ͳ�Ļ����л�����ġ������͡��ꡱ�������DZ����������е��Ļ��������Ļ�����.Ϊ�������㴫ͳ�Ļ���ijУΪ��������������塷�͡�ˮ䰴��������������ף�����ÿ�ס��������塷�������ļ۸��ÿ�ס�ˮ䰴����������ļ۸��60Ԫ����4800Ԫ����ˮ䰴�������������������3600Ԫ�����������塷������������2������ÿ�ס�ˮ䰴����������ļ۸�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD��CE�۵���ʹ��D����BC���ϵ�F������E��AD�ϣ�
��1����֤���ı���ABFEΪƽ���ı��Σ�
��2����AB=4��BC=6�����ı���ABFE���ܳ���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com