
【题目】如图,将ABCD沿CE折叠,使点D落在BC边上的F处,点E在AD上.
(1)求证:四边形ABFE为平行四边形;
(2)若AB=4,BC=6,求四边形ABFE的周长.

【答案】(1)证明见解析;(2)12.
【解析】
(1)根据折叠的性质得到EF=ED,∠CFE=∠CDE,根据平行四边形的性质得到AD∥BC,∠B=∠D,由平行线的判定得到AE∥BF,即可得到结论;
(2)根据平行四边形的性质得到EF=AB=4.求得ED=4,得到AE=BF=6-4=2,于是得到结论.
(1)证明:∵将ABCD沿CE折叠,使点D落在BC边上的F处,∴EF=ED,∠CFE=∠CDE,
∵四边形ABCD是平行四边形,∴AD∥BC,∠B=∠D,∴AE∥BF,∠B=∠CFE,
∴AB∥EF,∴四边形ABFE为平行四边形;
(2)解:∵四边形ABFE为平行四边形,∴EF=AB=4,
∵EF=ED,∴ED=4,∴AE=BF=6﹣4=2,∴四边形ABFE的周长=AB+BF+EF+EA=12.


科目:初中数学 来源: 题型:
【题目】如图,∠AOB=α,∠COD=β(α>β),OC与OB重合,OD在∠AOB外,射线OM、ON分别是∠AOC、∠BOD的角平分线.
(1)①若α=100°,β=60°,则∠MON等于多少;
②在①的条件下∠COD绕点O逆时针旋转n°(0<n<100(且n≠60)时,求∠MON的度数;
(2)直接写出∠COD绕点O逆时针旋转n°(0<n<360)时∠MON的值(用含α、β的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠AOB的度数为;∠A的度数为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长均为1个单位的正方形网格图中,建立了平面直角坐标系xOy,按要求解答下列问题:

(1)写出△ABC三个顶点的坐标;
(2)画出△ABC向右平移6个单位后得到的图形△A1B1C1;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列式子:
0×2+1=12……①
1×3+1=22……②
2×4+1=32……③
3×5+1=42……④
……
(1)第⑤个式子 ,第⑩个式子 ;
(2)请用含n(n为正整数)的式子表示上述的规律,并证明:
(3)求值:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C,D.
(1)∠PCD=∠PDC吗?为什么?
(2)OP是CD的垂直平分线吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,只用圆规找AB的中点P.
作法:
② 以A为圆心,AB长为半径作圆;
②以B为圆心,AB长为半径在圆上连续截取,记截点为B1 , B2 , B3 , B4 , B5;
③ 以B3为圆心,BB3长为半径画弧;以B为圆心,AB长为半径画弧,与前弧交于点C;
④以C为圆心,CB长为半径画弧交线段AB于点P.
结论:点P就是所求作的线段AB的中点.
(1)配合图形,理解作法,根据作图过程给予证明:点P是线段AB的中点.
(2)已知⊙O,请只用圆规把圆周四等分.(保留作图痕迹,不要求写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE是∠AOC的平分线,∠BOC=130°,∠BOF=140°,则∠EOF的度数为( )
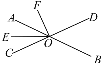
A. 95° B. 65°
C. 50° D. 40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com