
【题目】如图,⊙O是△ABC的外接圆,∠ABC=45°,OC∥AD,AD交BC的延长线于D,AB交OC于E.

(1)求证:AD是⊙O的切线;
(2)若⊙O的直径为6,线段BC=2,求∠BAC的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
试题(1)连接OA,要证明AD是⊙O的切线即要证明OA⊥AD,由∠ABC=45°可得出∠AOC=90°,由OC∥AD可得出∠OAD=90°,即证明出OA⊥AD;(2)延长CO交圆O于F,连接BF,要求sin∠BAC即要求sin∠F,因为直径CF,所以∠FBC=90°,所以得出sin∠BAC =sin∠F=![]() =
=![]() .
.
试题解析:
(1)证明:连接OA,
∵∠ABC=45°,
∴∠AOC=2∠ABC=90°,
∴OA⊥OC,
∵AD∥OC,
∴OA⊥AD,
∴AD是⊙O的切线.
(2)
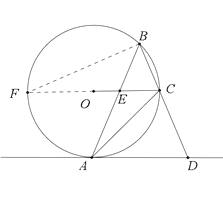
延长CO交圆O于F,连接BF,
∴∠F=∠BAC,
∵FC为直径,
∴∠FBC=90°,
∴sin∠BAC=sin∠F=![]() =
=![]() .
.


 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B. C.E在同一条直线上,连结DC.

(1)请在图2中找出与△ABE全等的三角形,并给予证明;
(2)证明:DC⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用![]() 元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高
元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高![]() 元,商店用了
元,商店用了![]() 元,所购数量是第一次的
元,所购数量是第一次的![]() 倍.
倍.
(1)求第一批采购的书包的单价是多少元?
(2)若商店按售价为每个书包![]() 元,销售完这两批书包,总共获利多少元?
元,销售完这两批书包,总共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm, BC=12cm.点P从点C处出发以1cm/s向A匀速运动,同时点Q从B点出发以2cm/s向C点匀速移动,若一个点到达目的停止运动时,另一点也随之停止运动.运动时间为t秒;

(1)用含有t的代数式表示BQ、CP的长;
(2)写出t的取值范围;
(3)用含有t的代数式 表示Rt△PCQ和四边形APQB的面积;
(4)当P、Q处在什么位置时,四边形PQBA的面积最小,并求这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(2k+3)+k2+3k-4=0.
(1) 试判断上述方程根的情况并说明理由;
(2) 若以上一元二次方程的两个根分别为![]() 、
、![]() (
(![]() ),
),
① m=________,n=_________;
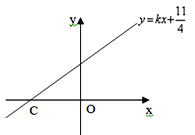
②当![]() 时,点A、B分别是直线
时,点A、B分别是直线![]() :y=kx+
:y=kx+![]() 上两点且A、B两点的横坐标分别为
上两点且A、B两点的横坐标分别为![]() 、
、![]() ,直线
,直线![]() 与
与![]() 轴相交于点C,若S△BOC=2S△AOC,求
轴相交于点C,若S△BOC=2S△AOC,求![]() 的值;
的值;
(3)在(2)的条件下,问在![]() 轴上是否存在点Q,使△ABQ的三个内角平分线交点在
轴上是否存在点Q,使△ABQ的三个内角平分线交点在![]() 轴上?若存在,求出点Q的坐标,若不存在,请说明理由.
轴上?若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.

(1)试说明:AD∥BC;
(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD在直角坐标系中,边BC在x轴上,B点坐标为(m,0)且m>0.AB=a,BC=b,且满足b=![]() .
.
(1)求a,b的值及用m表示出点D的坐标;
(2)连接OA,AC,若△OAC为等腰三角形,求m的值;
(3)△OAC能为直角三角形吗?若能,求出m的值;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,且EH=EB.下列四个结论:①∠ABC=45°;②AH=BC;③BE+CH=AE;④△AEC是等腰直角三角形.你认为正确的序号是( )

A. ①②③ B. ①③④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com