
分析 根据韦达定理可得x1+x2=-7,x1x2=-8,再分别代入到$\frac{x_{2}}{x_{1}}$+$\frac{x_{1}}{x_{2}}$=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{x}_{1}{x}_{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$、x12+x22=(x1+x2)2-2x1x2求值可得.
解答 解:∵x1、x2是方程2x2+14x-16=0的两实数根,
∴x1+x2=-7,x1x2=-8,
①$\frac{x_{2}}{x_{1}}$+$\frac{x_{1}}{x_{2}}$=$\frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{x}_{1}{x}_{2}}$=$\frac{({x}_{1}+{x}_{2})^{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{49+16}{-8}$=-$\frac{65}{8}$;
②x12+x22=(x1+x2)2-2x1x2=(-7)2-2×(-8)=65.
点评 本题主要考查根与系数的关系,熟练掌握韦达定理是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
| 星 期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | -0.29 | +0.06 | -0.12 | +0.24 | +0.06 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
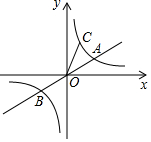 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4,双曲线y=$\frac{k}{x}$(k>0)上一点C的纵坐标为8,则点B的坐标为(-4,-2),△AOC的面积为15.
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4,双曲线y=$\frac{k}{x}$(k>0)上一点C的纵坐标为8,则点B的坐标为(-4,-2),△AOC的面积为15.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一农户要建一个矩形猪舍,猪舍的一边利用现有的住房墙,另外三边用25m长得建筑材料围成,为方便进出,在垂直于住房墙的一边留一个小门.
如图,一农户要建一个矩形猪舍,猪舍的一边利用现有的住房墙,另外三边用25m长得建筑材料围成,为方便进出,在垂直于住房墙的一边留一个小门.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com