
【题目】如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧![]() 的长为
的长为![]() ,直线
,直线![]() 与x轴、y轴分别交于点A、B.
与x轴、y轴分别交于点A、B.

(1)求证:直线AB与⊙O相切;
(2)求图中所示的阴影部分的面积(结果用π表示)
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)作OD⊥AB于D,由弧长公式和已知条件求出半径OM=![]() ,由直线解析式求出点A和B的坐标,得出OA=3,OB=4,由勾股定理求出AB=5,再由△AOB面积的计算方法求出OD,即可得出结论;
,由直线解析式求出点A和B的坐标,得出OA=3,OB=4,由勾股定理求出AB=5,再由△AOB面积的计算方法求出OD,即可得出结论;
(2)阴影部分的面积=△AOB的面积﹣扇形OMN的面积,即可得出结果.
试题解析:(1)证明:作OD⊥AB于D,如图所示:
∵劣弧![]() 的长为
的长为![]() ,∴
,∴![]() =
=![]() ,解得:OM=
,解得:OM=![]() ,即⊙O的半径为
,即⊙O的半径为![]() ,∵直线
,∵直线![]() 与x轴、y轴分别交于点A、B,当y=0时,x=3;当x=0时,y=4,∴A(3,0),B(0,4),∴OA=3,OB=4,∴AB=
与x轴、y轴分别交于点A、B,当y=0时,x=3;当x=0时,y=4,∴A(3,0),B(0,4),∴OA=3,OB=4,∴AB=![]() =5,∵△AOB的面积=
=5,∵△AOB的面积=![]() ABOD=
ABOD=![]() OAOB,∴OD=
OAOB,∴OD=![]() =
=![]() =半径OM,∴直线AB与⊙O相切;
=半径OM,∴直线AB与⊙O相切;
(2)解:图中所示的阴影部分的面积=△AOB的面积﹣扇形OMN的面积=![]() =
=![]() .
.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
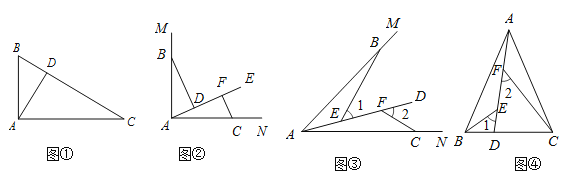
【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=![]() ,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
(1)特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
(2)归纳证明:如图③,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,∠1=∠2=∠BAC. 求证:△ABE≌△CAF;
(3)拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列不等式变形中,错误的是( )
A. 若 a≤b,则 a+c≤b+cB. 若 a+c≤b+c,则 a≤b
C. 若 a≤b,则 ac2≤bc2D. 若 ac2≤bc2,则 a≤b
查看答案和解析>>
科目:初中数学 来源: 题型:
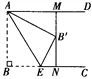
【题目】如图,已知AD∥BC,AB⊥BC,AB=3.点E为射线 BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大爷用280元买了甲、乙两种药材,甲种药材每千克20元,乙种药材每千克60元,且甲种药材比乙种药材多买了2千克,则甲种药材买了___千克.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com