
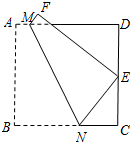
 如图,将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN.
如图,将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN.分析 (1)连接BM,EM,BE.由题设,得四边形ABNM和四边形FENM关于直线MN对称.由轴对称的性质知BM=EM,BN=EN.又有∠A=∠D=∠C=90°,设AB=BC=CD=DA=2.由$\frac{CE}{CD}$得,CE=DE=1;设BN=x,则NE=x,NC=2-x.在Rt△CNE中,由勾股定理可解得x的值,从而得以BN的值,在Rt△ABM和在Rt△DEM中,由勾股定理知AM2+AB2=BM2,DM2+DE2=EM2,有AM2+AB2=DM2+DE2.设AM=y,则可求得y的值,得到AM的值从而得到$\frac{AM}{BN}$.
(2)连接BE,$\frac{CE}{CD}$=$\frac{1}{n}$,令CD=CB=n,则CE=1,设BN=x,则EN=x,由勾股定理得x=$\frac{{n}^{2}+1}{2n}$;作MH⊥BC于H,可证得△EBC≌△NMH,由此得NH=1,从而可得$\frac{AM}{BN}$的值.
解答 解:(1)如图1,连接BM,EM,BE.
由题设,得四边形ABNM和四边形FENM关于直线MN对称.
∴MN垂直平分BE,
∴BM=EM,BN=EN.
∵四边形ABCD是正方形,
∴∠A=∠D=∠C=90°,
设AB=BC=CD=DA=2.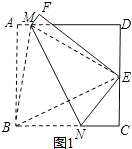
∵$\frac{CE}{CD}$=$\frac{1}{2}$,
∴CE=DE=1.
设BN=x,则NE=x,NC=2-x.
在Rt△CNE中,NE2=CN2+CE2.
∴x2=(2-x)2+12,
解得x=$\frac{5}{4}$,即BN=$\frac{5}{4}$.
在Rt△ABM和在Rt△DEM中,AM2+AB2=BM2,DM2+DE2=EM2,
∴AM2+AB2=DM2+DE2.
设AM=y,则DM=2-y,
∴y2+22=(2-y)2+12,
解得y=$\frac{1}{4}$,即AM=$\frac{1}{4}$,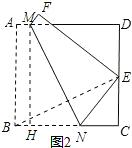
∴$\frac{AM}{BN}$=$\frac{1}{5}$.
(2)当四边形ABCD为正方形时,连接BE,$\frac{CE}{CD}$=$\frac{1}{n}$,
不妨令CD=CB=n,则CE=1,设BN=x,则EN=x,
EN2=NC2+CE2,
x2=(n-x)2+12,
x=$\frac{{n}^{2}+1}{2n}$;
如图2,作MH⊥BC于H,则MH=BC,
又点B,E关于MN对称,则MN⊥BE,∠EBC+∠BNM=90°;
∵∠NMH+∠BNM=90°,
∴∠EBC=∠NMH,
在△EBC和△NMH中,
$\left\{\begin{array}{l}{∠EBC=∠NMH}\\{∠MNH=∠BCE=90°}\\{MH=BC}\end{array}\right.$,
∴△EBC≌△NMH,
∴NH=EC=1,
AM=BH=BN-NH=$\frac{{n}^{2}+1}{2n}$-1=$\frac{{n}^{2}-2n+1}{2n}$,
则:$\frac{AM}{BN}$=$\frac{\frac{{n}^{2}-2n+1}{2n}}{\frac{{n}^{2}+1}{2n}}$=$\frac{{n}^{2}-2n+1}{{n}^{2}+1}$.
点评 本题考查图形的翻折变换,相似三角形的判定和性质以及勾股定理的综合应用,由于计算量较大,需要细心求解.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:解答题
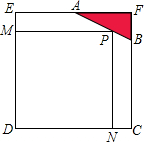 已知边长为4的正方形截取一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.若在AB上有一点P使矩形MPND的面积最大,请你求出此时矩形MPND的边长DN、PN.
已知边长为4的正方形截取一个角后成为五边形ABCDE(如图),其中AF=2,BF=1.若在AB上有一点P使矩形MPND的面积最大,请你求出此时矩形MPND的边长DN、PN.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ② | B. | ②③ | C. | ①② | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
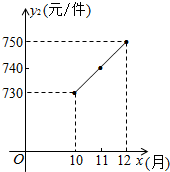 某企业为重庆计算机产业基地提供电脑配件,受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
某企业为重庆计算机产业基地提供电脑配件,受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
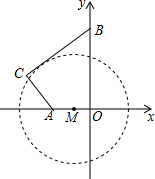 某地质公园为了方便游客,计划修建一条栈道BC连接两条进入观景台OA的栈道AC和OB,其中AC⊥BC,同时为减少对地质地貌的破坏,设立一个圆形保护区⊙M(如图所示),M是OA上一点,⊙M与BC相切,观景台的两端A、O到⊙M上任意一点的距离均不小于80米.经测量,OA=60米,OB=170米,tan∠OBC=$\frac{4}{3}$.
某地质公园为了方便游客,计划修建一条栈道BC连接两条进入观景台OA的栈道AC和OB,其中AC⊥BC,同时为减少对地质地貌的破坏,设立一个圆形保护区⊙M(如图所示),M是OA上一点,⊙M与BC相切,观景台的两端A、O到⊙M上任意一点的距离均不小于80米.经测量,OA=60米,OB=170米,tan∠OBC=$\frac{4}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com