
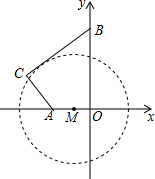
 某地质公园为了方便游客,计划修建一条栈道BC连接两条进入观景台OA的栈道AC和OB,其中AC⊥BC,同时为减少对地质地貌的破坏,设立一个圆形保护区⊙M(如图所示),M是OA上一点,⊙M与BC相切,观景台的两端A、O到⊙M上任意一点的距离均不小于80米.经测量,OA=60米,OB=170米,tan∠OBC=$\frac{4}{3}$.
某地质公园为了方便游客,计划修建一条栈道BC连接两条进入观景台OA的栈道AC和OB,其中AC⊥BC,同时为减少对地质地貌的破坏,设立一个圆形保护区⊙M(如图所示),M是OA上一点,⊙M与BC相切,观景台的两端A、O到⊙M上任意一点的距离均不小于80米.经测量,OA=60米,OB=170米,tan∠OBC=$\frac{4}{3}$.分析 (1)过C点作CE⊥OB于E,过A作AF⊥CE于F,设出AF,然后通过解直角三角形求得CE,进一步得到BE,然后由勾股定理得出答案;
(2)设BC与⊙M相切于Q,延长QM交直线BO于P,设OM=x,把PB、PQ用含有x的代数式不是,再结合观景台的两端A、O到⊙M上任意一点的距离均不小于80米列式求得x的范围,得到x取最小值时圆的半径最大,即圆形保护区的面积最大.
解答  解:(1)如图1,过C点作CE⊥OB于E,过A作AF⊥CE于F,
解:(1)如图1,过C点作CE⊥OB于E,过A作AF⊥CE于F,
∵∠ACB=90°∠BEC=90°,
∴∠ACF=∠CBE,
∴tan∠ACF=tan∠OBC=$\frac{4}{3}$,
设AF=4x,则CF=3x,
∵∠AOE=∠AFE=∠OEF=90°,
∴OE=AF=4x,EF=OA=60,
∴CE=3x+60,
∵tan∠OBC=$\frac{4}{3}$.
∴BE=$\frac{3}{4}$CE=$\frac{9}{4}$x+45,
∴OB=OE+BE=4x+$\frac{9}{4}$x+45,
∴4x+$\frac{9}{4}$x+45=170,
解得:x=20,
∴CE=120(米),BE=90(米),
∴BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=150(米).
(2)如图2,设BC与⊙M相切于Q,延长QM交直线BO于P,
∵∠POM=∠PQB=90°,
∴∠PMO=∠CBO,
∴tan∠OBC=$\frac{4}{3}$.
∴tan∠PMO=$\frac{4}{3}$.
设OM=x,则OP=$\frac{4}{3}$x,PM=$\frac{5}{3}$x,
∴PB=$\frac{4}{3}$x+170,
在RT△PQB中,tan∠PBQ=$\frac{PQ}{BQ}$=$\frac{4}{3}$.
∴$\frac{PQ}{PB}$=$\frac{4}{5}$,
∴PQ=$\frac{4}{5}$($\frac{4}{3}$x+170)=$\frac{16}{15}$x+136,
设⊙M的半径为R,
∴R=MQ=$\frac{16}{15}$x+136-$\frac{5}{3}$x=136-$\frac{3}{5}$x,
∵A、O到⊙M上任意一点的距离均不小于80米,
∴R-AM≥80,R-OM≥80,
∴136-$\frac{3}{5}$x-(60-x)≥80,136-$\frac{3}{5}$x-x≥80,
解得:10≤x≤35,
∴当且仅当x=10时R取最大值,
∴OM=10米时,保护区的面积最大.
点评 本题考查了圆的切线,考查了直线和圆的位置关系,解题的关键在于对题意的理解.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:解答题
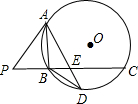 如图,已知PA是⊙O的切线,切点为A,PC与⊙O相交于B,C点,且AB⊥PC于点B,点D为$\widehat{BC}$上一点,连接AD于点E,且∠PAB=∠DAB.
如图,已知PA是⊙O的切线,切点为A,PC与⊙O相交于B,C点,且AB⊥PC于点B,点D为$\widehat{BC}$上一点,连接AD于点E,且∠PAB=∠DAB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
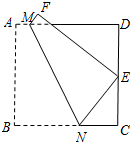 如图,将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN.
如图,将正方形纸片ABCD折叠,使点B落在CD边上一点E(不与点C,D重合),压平后得到折痕MN.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
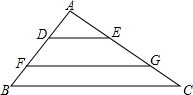 如图所示,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形BCGF,则DE:BC等于( )
如图所示,DE∥FG∥BC,且S△ADE=S四边形DFGE=S四边形BCGF,则DE:BC等于( )| A. | 1:2 | B. | 1:4 | C. | 1:$\sqrt{3}$ | D. | 1:$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
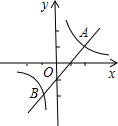 如图,函数y1=x-1与y2=$\frac{2}{x}$的图象交于点A(2,1),B(-1,-2),则使y1>y2的x的范围是( )
如图,函数y1=x-1与y2=$\frac{2}{x}$的图象交于点A(2,1),B(-1,-2),则使y1>y2的x的范围是( )| A. | x>2 | B. | -1<x<0或x>2 | C. | -1<x<2 | D. | x<-1或x>2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com