
����Ŀ��ij�ҵ������̳ǵ��������ۼ�Ϊÿ̨2100Ԫ���յ������ۼ�Ϊÿ̨1750Ԫ��ÿ̨�����Ľ��۱�ÿ̨�յ��Ľ��۶�400Ԫ���̳���80000Ԫ������������������64000Ԫ�����յ���������ȣ�
��1����ÿ̨�������յ��Ľ��۷ֱ��Ƕ��٣�
��2�������̳���һ�ι��������ּҵ繲100̨���蹺�������x̨����100̨�ҵ������������ΪyԪ��Ҫ���յ����������������������2������������13000Ԫ������������ķ������ж����֣���ȷ���������ķ����Լ��������
��3��ʵ�ʽ���ʱ�����ҶԵ����������µ�k��0��k��100��Ԫ�����̵걣�������ּҵ���ۼ۲��䣬�������������Ϣ����2��������������Ƴ�ʹ��100̨�ҵ��������������Ľ���������
���𰸡���1��ÿ̨�յ��Ľ���Ϊ1600Ԫ����ÿ̨�����Ľ���Ϊ2000Ԫ��
��2�������ķ�������7�֣������������34̨���յ�66̨��������������Ϊ13300Ԫ��
��3����50��k��100ʱ�����������40̨���յ�60̨�������������0��k��50ʱ�����������34̨���յ�66̨�������������k=50ʱ��ÿ�ֽ���������������һ����
��������
�����������1����������ÿ̨�յ��Ľ���ΪxԪ����ÿ̨�����Ľ���Ϊ��x+400��Ԫ���������̳���80000Ԫ������������������64000Ԫ�����յ�����������з��̣��ⷽ��.
��2����Ŀ������Ҫ����������13000Ԫ�������յ����������������������2��������ʵ�������յ�����������ȡ����������������Ҫ����һ���ǣ�����=�������������ۼ�-��������������������=����������+�յ������õ�y����x��һ�κ��������ݵڶ���Ҫ���г�����ʽ����һ������Ҫ��ķ�Χ���ҵ�������.
��3�������������µ���kԪ������ÿ̨�������������kԪ�������������������y����x��һԪһ�κ������ɺ�������ʽ��һ�κ��������ʿ�֪������������ֵ��k-50�������Ծ������ڴ˷������������.
�����������1����ÿ̨�յ��Ľ���ΪxԪ����ÿ̨�����Ľ���Ϊ��x+400��Ԫ����������ã�![]() ����ã�x=1600�������飬x=1600��ԭ���̵Ľ⣬x+400=1600+400=2000��
����ã�x=1600�������飬x=1600��ԭ���̵Ľ⣬x+400=1600+400=2000��
��ÿ̨�յ��Ľ���Ϊ1600Ԫ����ÿ̨�����Ľ���Ϊ2000Ԫ��
��2���蹺�������x̨����100̨�ҵ������������ΪyԪ����y=��2100��2000��x+��1750��1600����100��x��=��50x+15000����������ã�![]() ����ã�
����ã�![]() ����xΪ����������x=34��35��36��37��38��39��40���������ķ�������7�֣����������34̨���յ�66̨���������35̨���յ�65̨���������36̨���յ�64̨���������37̨���յ�63̨���������38̨���յ�62̨���������39̨���յ�61̨���������40̨���յ�60̨��
����xΪ����������x=34��35��36��37��38��39��40���������ķ�������7�֣����������34̨���յ�66̨���������35̨���յ�65̨���������36̨���յ�64̨���������37̨���յ�63̨���������38̨���յ�62̨���������39̨���յ�61̨���������40̨���յ�60̨��
��y=��50x+15000��k=��50��0����y��x�����������
����x=34ʱ��y�����ֵ�����ֵΪ����50��34+15000=13300��Ԫ����
�𣺵����������34̨���յ�66̨��������������Ϊ13300Ԫ��
��3�������ҶԵ����������µ�k��0��k��100��Ԫ�����̵걣�������ּҵ���ۼ۲��䣬
������y=��2100��2000+k��x+��1750��1600����100��x��=��k��50��x+15000��
��k��50��0����50��k��100ʱ��y��x�������������![]() ������x=40ʱ����100̨�ҵ�����������������������40̨���յ�60̨��
������x=40ʱ����100̨�ҵ�����������������������40̨���յ�60̨��
��k��50��0����0��k��50ʱ��y��x���������С����![]() ������x=34ʱ����100̨�ҵ�����������������������34̨���յ�66̨��
������x=34ʱ����100̨�ҵ�����������������������34̨���յ�66̨��
��k=50ʱ��ÿ�ֽ���������������һ����
�𣺵�50��k��100ʱ�����������40̨���յ�60̨�������������0��k��50ʱ�����������34̨���յ�66̨�������������k=50ʱ��ÿ�ֽ���������������һ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1�е�Ħ���ֿɳ����һ��Բ��Բ��һ�������ĸ߶�y��m������תʱ��x��min��֮��Ĺ�ϵ��ͼ2��ʾ������ͼ�е���Ϣ���ش����⣺
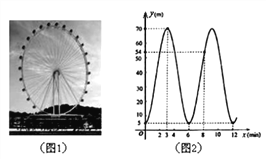
��1������ͼ2��ȫ����

��2�������ӳ�����������У��Ա����� ��������� ��
��3������ͼ��Ħ���ֵ�ֱ��Ϊ m������תһ����Ҫ��ʱ��Ϊ min��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����·MN��·PQ�ڵ�O�����㣬��QON=30������·PQ��A����O��240�ף��������ʻʱ����Χ200�����ڻ��ܵ�������Ӱ�죬��ô������·MN����ON������72ǧ��/ʱ���ٶ���ʻʱ����A��������Ӱ���ʱ�䡣

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����(x+2)2-(x+1)(x-1),����x=1.5
��2����a+b����a��b����b��a��b��������a=��2��b=1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� ��һ����ͯ��ǰϦ��ޭ���ؽ������������ض�ͯ����һ��ѧϰ��Ʒ���ȶ��Ȫ���ȪСѧ�����ض�ͯ�������г���ͳ�ƣ����ָ������ض�ͯ�����ֱ�Ϊ6 ����7 ����8 ����10 ����12 �����������Σ�����ͳ�ƽ�����Ƴ�����ͼ��ʾ��������������ͳ��ͼ��
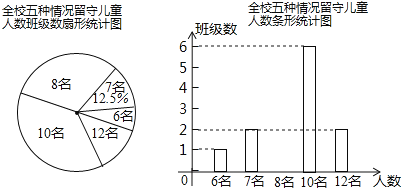
���������ͳ��ͼ������������⣺
��1����У�ж��ٸ��༶������ȫ����ͳ��ͼ��
��2����Уƽ��ÿ���ж��������ض�ͯ�����ض�ͯ�����������Ƕ��٣�
��3������������Сѧ����60 ����ѧ�࣬������������ݣ����Ƹ���Сѧ���У����ж��������ض�ͯ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�EΪBC���е㣬����AE���ӳ���DC���ӳ����ڵ�F.
(1)��֤��AB��CF��
(2)��BC��AF����ʲô������ϵʱ���ı���ABFC�Ǿ��Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ε������ڽǵĺ���85������ô�����������(����)
A. �۽������� B. ֱ�������� C. ��������� D. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB=AC=12���ף�BC=9���ף���DΪAB���е㣮�����P���߶�BC����3����/����ٶ���B��C���˶���ͬʱ��Q���߶�CA����C����A���˶���
��1������Q���˶��ٶ����P���˶��ٶ���ȣ�1����ʱ����BPD����CQP�Ƿ�ȫ�ȣ���˵����
��2����Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD�ա�CPQ��
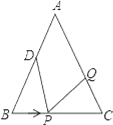
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com