练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若三角形的两个内角的和是85°，那么这个三角形是(　　)

    A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 不能确定

    【答案】A

    【解析】试题分析：根据三角形的内角和定理可得：另外一个内角的度数为95°，则这个三角形就是钝角三角形，故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】定义：如果一元二次方程ax2+bx+c=0（a≠0）满足a+b+c=0，那么我们称这个方程为“至和”方程；如果一元二次方程ax2+bx+c=0（a≠0）满足a﹣b+c=0那么我们称这个方程为“至美”方程，如果一个一元二次方程既是“至和”方程又是“至美”方程我们称之为“和美方程”．对于“和美方程”，下列结论正确的是（ ）

    A. 方程两根之和等于0

    B. 方程有一根等于0

    C. 方程有两个相等的实数根

    D. 方程两根之积等于0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知2x=3，2y=5．求：

    （1）2x+y的值； （2）23x的值； （3）22x+y﹣1的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某家电销售商城电冰箱的销售价为每台2100元，空调的销售价为每台1750元，每台电冰箱的进价比每台空调的进价多400元，商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等．

    （1）求每台电冰箱与空调的进价分别是多少？

    （2）现在商城准备一次购进这两种家电共100台，设购进电冰箱x台，这100台家电的销售总利润为y元，要求购进空调数量不超过电冰箱数量的2倍，总利润不低于13000元，请分析合理的方案共有多少种？并确定获利最大的方案以及最大利润；

    （3）实际进货时，厂家对电冰箱出厂价下调k（0＜k＜100）元，若商店保持这两种家电的售价不变，请你根据以上信息及（2）问中条件，设计出使这100台家电销售总利润最大的进货方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】老师对甲、乙两人的五次数学测验成绩进行统计，得出两人五次测验成绩的平均分均为90分，方差分别是S2甲=51、S2乙=12，由此可知（　　）

    A. 甲比乙的成绩稳定B. 乙比甲的成绩稳定

    C. 甲、乙两人的成绩一样稳定D. 无法确定谁的成绩更稳定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将矩形OABC置于平面直角坐标系中，点A的坐标为（0，4），点C在x轴上，点D（，1）在BC上，将矩形OABC沿AD折叠压平，使点B落在坐标平面内，设点B的对应点为点E．若抛物线（a≠0且a为常数）的顶点落在△ADE的内部，则a的取值范围是（ ）

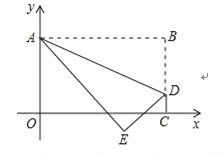
    A． B． C． D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某商场为了吸引顾客，设立了一个可以自由转动的转盘，并规定：每购买500元商品，就能获得一次转动转盘的机会，如果转盘停止后，指针上对准500、200、100、50、10的区域，顾客就可以获得500元、200元、100元、50元、10元的购物券一张（转盘等分成20份）。

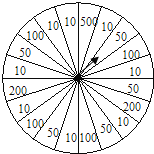
    （1）小华购物450元，他获得购物券的概率是多少？

    （2）小丽购物600元，那么：

    ① 她获得50元购物券的概率是多少？

    ② 她获得100元以上（包括100元）购物券的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD中，BD⊥AD，∠A=45°，E、F分别是AB，CD上的点，且BE=DF，连接EF交BD于O．

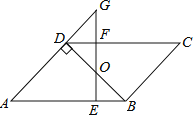
    （1）求证：BO=DO；

    （2）若EF⊥AB，延长EF交AD的延长线于G，当FG=1时，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程x2﹣mx+3=0的解为﹣1，则m的值为（　　）

    A. ﹣4 B. 4 C. ﹣2 D. 2

    查看答案和解析>>

    同步练习册答案