
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
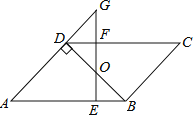
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
【答案】(1)证明见解析,(2)2![]() .
.
【解析】
试题分析:(1)通过证明△ODF与△OBE全等即可求得.
(2)由△ADB是等腰直角三角形,得出∠A=45°,因为EF⊥AB,得出∠G=45°,所以△ODG与△DFG都是等腰直角三角形,从而求得DG的长和EF=2,然后等腰直角三角形的性质即可求得.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB,
∴∠ODF=∠OBE,
在△ODF与△OBE中
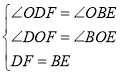
∴△ODF≌△OBE(AAS)
∴BO=DO;
(2)解:∵BD⊥AD,
∴∠ADB=90°,
∵∠A=45°,
∴∠DBA=∠A=45°,
∵EF⊥AB,
∴∠G=∠A=45°,
∴△ODG是等腰直角三角形,
∵AB∥CD,EF⊥AB,
∴DF⊥OG,
∴OF=FG,△DFG是等腰直角三角形,
∵△ODF≌△OBE(AAS)
∴OE=OF,
∴GF=OF=OE,
即2FG=EF,
∵△DFG是等腰直角三角形,
∴DF=FG=1,∴DG=![]() =DO,
=DO,
∴在等腰RT△ADB 中,DB=2DO=2![]() =AD
=AD
∴AD=2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°,公路PQ上A处距O点240米,如果火车行驶时,周围200米以内会受到噪音的影响,那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,求A处受噪音影响的时间。

查看答案和解析>>
科目:初中数学 来源: 题型:
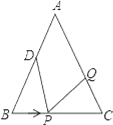
【题目】如图,已知△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B向C点运动,同时点Q在线段CA上由C点向A点运动.
(1)若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP是否全等,请说明;
(2)点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?
查看答案和解析>>
科目:初中数学 来源: 题型:
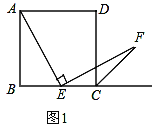
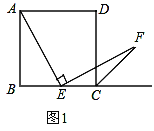
【题目】如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.
(1)求证:AE=EF.
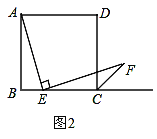
(2)如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点 ”其余条件不变,那么结论AE=EF是否成立呢?若成立,请你证明这一结论,若不成立,请你说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桥梁上的拉杆,电视塔的底座,都是三角形结构,而活动挂架是四边形结构,这是分别利用三角形和四边形的________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.
(1)求证:AE=EF.
(2)如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点 ”其余条件不变,那么结论AE=EF是否成立呢?若成立,请你证明这一结论,若不成立,请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在直角坐标系中,已知![]() 、
、![]() 、
、![]() 三点,其中
三点,其中![]() 、
、![]() 、
、![]() 满足关系式
满足关系式![]() ,
, ![]() ≤
≤![]() .
.
(1)![]() =_______;
=_______; ![]() =________;
=________; ![]() =_______.
=_______.
(2)如果点![]() 是第二象限内的一个动点,坐标为
是第二象限内的一个动点,坐标为![]() .将四边形
.将四边形![]() 的面积用
的面积用![]() 表示,请你写出
表示,请你写出![]() 关于
关于![]() 的函数表达式,并写出自变量的取值范围.
的函数表达式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点![]() ,使得四边形的面积
,使得四边形的面积![]() 与
与![]() 的面积相等?若存在,请求出点
的面积相等?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com