
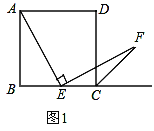
【题目】如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.
(1)求证:AE=EF.
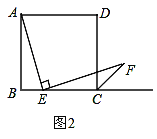
(2)如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点 ”其余条件不变,那么结论AE=EF是否成立呢?若成立,请你证明这一结论,若不成立,请你说明理由.
【答案】(1)证明见解析;(2)成立,证明见解析
【解析】试题分析:(1)取AB的中点G,连接EG,根据已知条件利用ASA判定△AME≌△ECF,因为全等三角形的对应边相等,所以AE=EF.
(2)在AB上取一点M,使AM=EC,连接ME,根据已知条件利用ASA判定△AME≌△ECF,因为全等三角形的对应边相等,所以AE=EF.
试题解析:
(1)证明:取AB的中点G,连接EG
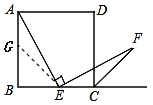
∵四边形ABCD是正方形∴AB=BC,∠B=∠BCD=∠DCG=90°
∵点E是边BC的中点
∴AM=EC=BE
∴∠BGE=∠BEG=45°
∴∠AGE=135°,
∵CF平分∠DCG,
∴∠DCF=∠FCG=45°,
∴∠ECF=180°-∠FCG=135°,
∴∠AGE=∠ECF
∵∠AEF=90°
∴∠AEB+∠CEF=90°,
又∵∠AEB+∠GAE=90°,
∴∠GAE=∠CEF,
在△AGE和△ECF中,∠GAE=∠CEF,AG=CE,∠AGE=∠ECF∴△AGE≌△ECF(ASA),∴AE=EF
(2)证明:在AB上取一点M,使AM=EC,连结ME,

∴BM=BE∴∠BME=45°∴∠AME=135°.
∵CF是外角平分线,
∴∠DCF = 45°.
∴∠ECF = 135°.
∴∠AME = ∠ECF .
∵∠AEB +∠BAE=90°,∠AEB + ∠CEF = 90°,
∴∠BAE = ∠CEF.
∴△AME ≌ △ECF(ASA).
∴AE=EF.


科目:初中数学 来源: 题型:
【题目】如图,某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定:每购买500元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针上对准500、200、100、50、10的区域,顾客就可以获得500元、200元、100元、50元、10元的购物券一张(转盘等分成20份)。
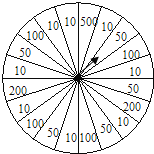
(1)小华购物450元,他获得购物券的概率是多少?
(2)小丽购物600元,那么:
① 她获得50元购物券的概率是多少?
② 她获得100元以上(包括100元)购物券的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.
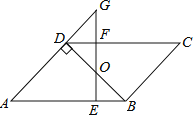
(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为6cm,当OP=6cm时,点P在_________;当OP__________时,点P在圆内;当OP___________时,点P不在圆外.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏和小聪进行百米赛跑,小敏每秒跑6.3米,小聪每秒跑7.1米,小聪让小敏先跑5米,则比赛结果是( )
A.小敏和小聪同时到达终点
B.小敏比小聪早近1秒到达终点
C.小敏比小聪晩近1秒到达终点
D.小敏比小聪晩近0.9秒到达终点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=2cm,BC=4cm,若以点C为圆心,2cm为半径作圆,则点A在⊙C____________,点B在⊙C____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用![]() 表示不大于
表示不大于![]() 的最大整数,例如:
的最大整数,例如: ![]() ,
, ![]() ,
, ![]() ;用
;用![]() 表示大于
表示大于![]() 的最小整数,例如:
的最小整数,例如: ![]() ,
, ![]() ,
, ![]() .解决下列问题:
.解决下列问题:
(1)![]() = ,,
= ,, ![]() = ;
= ;
(2)若![]() =2,则
=2,则![]() 的取值范围是 ;若
的取值范围是 ;若![]() =-1,则
=-1,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
, ![]() 满足方程组
满足方程组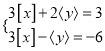 ,求
,求![]() ,
, ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com