等腰三角形的两边长分别为41cm和18cm,则该三角形的面积为________.
360cm
2分析:分41是底边与腰长两种情况讨论,再根据三角形的任意两边之和大于第三边判断,然后利用勾股定理求出等腰三角形底边上的高,再根据三角形的面积公式列式计算即可得解.
解答:
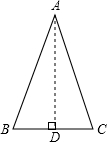
解:①41cm是底边时,腰长为18cm,
∵18+18=36<41,
∴此时不能组成三角形,
②41cm是腰长时,底边为18cm,
三角形的三边为41cm、41cm、18cm,
能够组成三角形,
如图,过点A作AD⊥BC,
则BD=

×18=9cm,
根据勾股定理,AD=

=
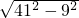
=40cm,
所以,该三角形的面积=

×18×40=360cm
2.
故答案为:360cm
2.
点评:本题考查了勾股定理,等腰三角形的性质,三角形的三边关系,难点在于要分情况讨论并利用三角形三边关系作出判断.

 解:①41cm是底边时,腰长为18cm,
解:①41cm是底边时,腰长为18cm, ×18=9cm,
×18=9cm, =
=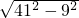 =40cm,
=40cm, ×18×40=360cm2.
×18×40=360cm2.
