
【题目】如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F:y=x2-2mx+m2-2与直线x=-2交于点P.
(1)当抛物线F经过点C时,求它的解析式;
(2)设点P的纵坐标为yP,求yP的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤-2,比较y1与y2的大小.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=12cm,CA⊥AB于点A,DB⊥AB于点B,且AC=4cm,点P从点B向点A运动,每秒钟走1cm,点Q从点B向点D运动,每秒钟走2cm,两点同时出发,运动几秒钟后,△CPA与△PQB全等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:身高在选定标准的±2%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级500名男生中随机选出10名男生,分别测量出他们的身高(单位:cm)收集并整理统计表:
男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
身高 | 163 | 171 | 173 | 159 | 161 | 174 | 164 | 166 | 169 | 164 |
根据以上表格信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你选择其中一个统计量作为选定标准,估计该校九年级男生中具有“普通身高”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知△ABC,以AB、AC为边向△ABC外作等边三角形ABD和等边三角形ACE,连接BE、CD.请你完成图形,并证明:BE=CD;

(2)如图(2),已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE、CD,BE和CD有什么数量关系?说明理由;
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图(3),要测量河两岸相对的两点B、E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=1千米,AC=AE.求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt ABC中,![]() ,AB=5cm, AC=3cm, 动点P从点B出发沿射线BC以2cm/s 的速度移动,设运动的时间为t秒.t= __________ 时三角形ABP为直角三角形.
,AB=5cm, AC=3cm, 动点P从点B出发沿射线BC以2cm/s 的速度移动,设运动的时间为t秒.t= __________ 时三角形ABP为直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
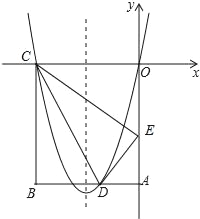
【题目】如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求点E坐标及经过O,D,C三点的抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(2)中的抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com