
【题目】如图,已知AB=12cm,CA⊥AB于点A,DB⊥AB于点B,且AC=4cm,点P从点B向点A运动,每秒钟走1cm,点Q从点B向点D运动,每秒钟走2cm,两点同时出发,运动几秒钟后,△CPA与△PQB全等?

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为( )

A. 5B. 6C. 8D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:四条边对应相等,四个角对应相等的两个四边形全等.某学习小组在研究后发现判定两个四边形全等需要五组对应条件,于是把五组条件进行分类研究,并且针对二条边和三个角对应相等类型进行研究提出以下几种可能:

①AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1;
②AB=A1B1,AD=A1D1,∠A=∠A1,∠B=∠B1,∠D=∠D1;
③AB=A1B1,AD=A1D1,∠B=∠B1,∠C=∠C1,∠D=∠D1;
④AB=A1B1,CD=C1D1,∠A=∠A1,∠B=∠B1,∠C=∠C1.
其中能判定四边形ABCD和四边形A1B1C1D1全等的有_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(a+b)x+ab-1=0,x1、x2是此方程的两个实数根,现给出三个结论:①x1≠x2;②x1x2<ab;③![]() +
+![]() <a2+b2.则正确结论的序号是______.(填上你认为正确的所有序号)
<a2+b2.则正确结论的序号是______.(填上你认为正确的所有序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等圆⊙O1 和⊙O2 相交于A,B两点,⊙O2 经过⊙O1 的圆心O1,两圆的连心线交⊙O1于点M,交AB于点N,连接BM,已知AB=2![]() .
.
求证:(1)BM是⊙O2的切线;
(2)求弧AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
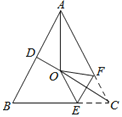
A. 60° B. 55° C. 50° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F:y=x2-2mx+m2-2与直线x=-2交于点P.
(1)当抛物线F经过点C时,求它的解析式;
(2)设点P的纵坐标为yP,求yP的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤-2,比较y1与y2的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com