
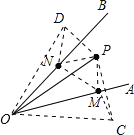
【题目】如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为( )

A. 5B. 6C. 8D. 10
【答案】C
【解析】
设点P关于OA的对称点为C,关于OB的对称点为D,当点M、N在CD上时,△PMN的周长最小.
解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM=CM,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PN=DN,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=8cm,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=OD=8.
∴△PMN的周长的最小值=PM+MN+PN=CM+MN+DN≥CD=8,
故选:C.


科目:初中数学 来源: 题型:
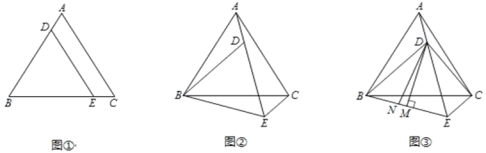
【题目】已知:如图①,△ABC是等边三角形,点D、E分别在边AB、BC上,且BD=BE,连接DE.
(1)求证:DE∥AC;
(2)将图①中的△BDE绕点B顺时针旋转,使得点A、D、E在同一条直线上,如图②,求∠AEC的度数;
(3)在(2)的条件下,如图③,连接CD,过点D作DM⊥BE于点M,在线段BM上取点N,使得∠DNE+∠DCE=180°.请探索三条线段EN,MN,EC之间的关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A点的坐标为(m,3),AB⊥x轴于点B,tan∠OAB=![]() ,反比例函数y1=
,反比例函数y1=![]() 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.
(1)求反比例函数解析式;
(2)设直线OA的解析式为y2=nx,请直接写出y1<y2时,自变量x的取值范围 .
(3)如图2,若函数y=3x与y1=![]() 的图象的另一支交于点M,求△OMB与四边形OCDB的面积的比值.
的图象的另一支交于点M,求△OMB与四边形OCDB的面积的比值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以正方形ABCD的边AB为直径作⊙O,E是⊙O上的一点,EF⊥AB于F,AF>BF,作直线DE交BC于点G.若正方形的边长为10,EF=4.
(1)分别求AF、BF的长.
(2)求证:DG是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.
(1)求m的取值范围.
(2)若2(x1+x2)+ x1x2+10=0.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=12cm,CA⊥AB于点A,DB⊥AB于点B,且AC=4cm,点P从点B向点A运动,每秒钟走1cm,点Q从点B向点D运动,每秒钟走2cm,两点同时出发,运动几秒钟后,△CPA与△PQB全等?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com