
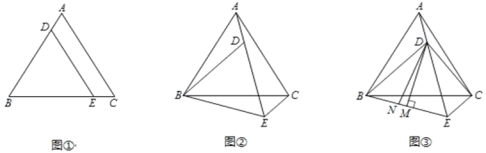
【题目】已知:如图①,△ABC是等边三角形,点D、E分别在边AB、BC上,且BD=BE,连接DE.
(1)求证:DE∥AC;
(2)将图①中的△BDE绕点B顺时针旋转,使得点A、D、E在同一条直线上,如图②,求∠AEC的度数;
(3)在(2)的条件下,如图③,连接CD,过点D作DM⊥BE于点M,在线段BM上取点N,使得∠DNE+∠DCE=180°.请探索三条线段EN,MN,EC之间的关系,并证明你的结论.
【答案】(1)见解析;(2)60°;(3)见解析.
【解析】
(1)由△ABC是等边三角形得∠B=60°,再由BD=BE,得△BDE是等边三角形,所以∠BED=∠C=60°,可得DE∥AC;
(2)由旋转,易证△BAD≌△BCE,所以∠BEC=∠BDA=180°-∠BDE=120°,所以∠AEC=∠BEC-∠BED=60°.
(3)在四边形CDNE中, 由(2)中∠NEC=120°易得∠NDC=60°,然后利用角边角证明△BDN≌△EDC,得出BN=EC,然后在BE边上利用线段关系可推出关系式.
证明:(1)∵△ABC为等边三角形,∴∠B=∠C=60°,
又∵BD=BE,∴△BDE为等边三角形,∴∠BEC=60°,
∴∠BEC=∠C,∴DE∥AC.
(2)∵∠ABD+∠DBC=60°,∠CBE+∠DBC=60°
∴∠ABD=∠CBE
在△ABD和△CBE中,
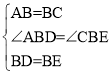
∴△ABD≌△CBE(SAS)
∴∠BEC=∠BDA,
又∵A、D、E在一条直线,
∴∠BDA+∠BDE=180°,
又∵∠BDE=60°,∴∠BDA=∠BEC=120°,
∴∠AEC=∠BEC-∠BED=120°-60°=60°
(3)在四边形CDNE中,∵∠DNE+∠DCE=180°
∴∠NDC+∠NEC=180°,
由(2)可知∠NEC=120°,∴∠NDC=60°
∴∠CDE+∠NDE=60°,
∵∠BDN+∠NDE=60°,
∴∠BDN=∠CDE
在△BDN和△EDC中,
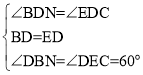
∴△BDN≌△EDC(ASA)
∴BN=EC
在等边△BDE中,DM⊥BE,
∴BM=ME
∴EN=MN+ME=MN+BM=MN+BN+MN=2MN+EC
故EN,MN,EC之间的关系的关系是EN=2MN+EC.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB,延长AC至E,使CE=AC.
(1)求证:DE=DB;
(2)连接BE,试判断△ABE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向运动,连接
方向运动,连接![]() ,以
,以![]() 为边,在
为边,在![]() 右侧按如图方式作等边
右侧按如图方式作等边![]() ,当点P从点E运动到点A时,求点F运动的路径长?
,当点P从点E运动到点A时,求点F运动的路径长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MAN是一钢架,为了使钢架更加坚固,需要在其内部添加一些钢管BC,CD,DE……,添加的钢管长度都与AB相等,若只能添加这样的钢管4根,则∠MAN的范围____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国![]() 道路交通安全法
道路交通安全法![]() 第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”
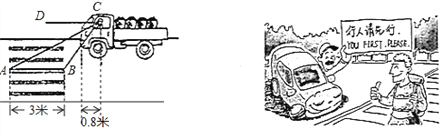
第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行” ![]() 如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是
如图:一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是![]() 和
和![]() ,如果斑马线的宽度是
,如果斑马线的宽度是![]() 米,驾驶员与车头的距离是
米,驾驶员与车头的距离是![]() 米,这时汽车车头与斑马线的距离x是多少?
米,这时汽车车头与斑马线的距离x是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,一次函数![]() 与x轴、y轴分别交于点A和点B,A点坐标为(3,0),∠OAB=45°.
与x轴、y轴分别交于点A和点B,A点坐标为(3,0),∠OAB=45°.

(1)求一次函数的表达式;
(2)点P是x轴正半轴上一点,以P为直角顶点,BP为腰在第一象限内作等腰Rt△BPC,连接CA并延长交y轴于点Q.
①若点P的坐标为(4,0),求点C的坐标,并求出直线AC的函数表达式;
②当P点在x轴正半轴运动时,Q点的位置是否发现变化?若不变,请求出它的坐标;如果变化,请求出它的变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB⊥BD,sinA=![]() ,将ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y=
,将ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y=![]() (k>0)同时经过B、D两点,则点B的坐标是_____.
(k>0)同时经过B、D两点,则点B的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为( )

A. 5B. 6C. 8D. 10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com