
【题目】如图,在等边![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向运动,连接
方向运动,连接![]() ,以
,以![]() 为边,在
为边,在![]() 右侧按如图方式作等边
右侧按如图方式作等边![]() ,当点P从点E运动到点A时,求点F运动的路径长?
,当点P从点E运动到点A时,求点F运动的路径长?

【答案】8
【解析】
连结DE,作FH⊥BC于H,如图,根据等边三角形的性质得∠B=60°,过D点作DE′⊥AB,则BE′=![]() BD=2,则点E′与点E重合,所以∠BDE=30°,DE=
BD=2,则点E′与点E重合,所以∠BDE=30°,DE=![]() ,接着证明△DPE≌△FDH得到FH=DE=2
,接着证明△DPE≌△FDH得到FH=DE=2![]() ,于是可判断点F运动的路径为一条线段,此线段到BC的距离为2
,于是可判断点F运动的路径为一条线段,此线段到BC的距离为2![]() ,当点P在E点时,作等边三角形DEF1,则DF1⊥BC,当点P在A点时,作等边三角形DAF2,作F2Q⊥BC于Q,则△DF2Q≌△ADE,所以DQ=AE=8,所以F1F2=DQ=8,于是得到当点P从点E运动到点A时,点F运动的路径长为8.
,当点P在E点时,作等边三角形DEF1,则DF1⊥BC,当点P在A点时,作等边三角形DAF2,作F2Q⊥BC于Q,则△DF2Q≌△ADE,所以DQ=AE=8,所以F1F2=DQ=8,于是得到当点P从点E运动到点A时,点F运动的路径长为8.
连结DE,作FH⊥BC于H,如图,
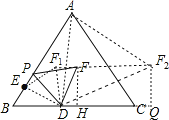
∵△ABC为等边三角形,
∴∠B=60°,
过D点作DE′⊥AB,则BE′=![]() BD=2,
BD=2,
∴点E′与点E重合,
∴∠BDE=30°,DE=![]() BE=2
BE=2![]() ,
,
∵△DPF为等边三角形,
∴∠PDF=60°,DP=DF,
∴∠EDP+∠HDF=90°
∵∠HDF+∠DFH=90°,
∴∠EDP=∠DFH,
在△DPE和△FDH中,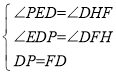 ,
,
∴△DPE≌△FDH,
∴FH=DE=2![]() ,
,
∴点P从点E运动到点A时,点F运动的路径为一条线段,此线段到BC的距离为2![]() ,
,
当点P在E点时,作等边三角形DEF1,∠BDF1=30°+60°=90°,则DF1⊥BC,
当点P在A点时,作等边三角形DAF2,作F2Q⊥BC于Q,则△DF2Q≌△ADE,所以DQ=AE=10-2=8,
∴F1F2=DQ=8,
∴当点P从点E运动到点A时,点F运动的路径长为8.


科目:初中数学 来源: 题型:
【题目】一位运动员在距篮下4m处跳起投篮,球运行的路线是抛物线,当球运行的水平距离是2.5m时,达到最大高度3.5m,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05m.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式.
(2)该运动员身高1.8m,在这次跳投中,球在头顶上0.25m处出手,
问:球出手时,他距离地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长是2,以BC边上的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形,得到第二个等边△AB2C2;再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形,得到第三个等边△AB3C3;…,记△B1CB2的面积为S1,△B2C1B3的面积为S2,△B3C2B4的面积为S3,如此下去,则Sn=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠C=90°,AC=BC=7,D是AB的中点,点E在AC上,点F在BC上,DE=DF,若BF=4,则EF=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.

(1)当t为何值时,CP把△ABC的周长分成相等的两部分;
(2)当t为何值时,CP把△ABC的面积分成相等的两部分;
(3)在(2)的情况下,若过点P作PE//BC,且在BC上有一点F,PE=CF,连结PF,
BE,试探索PF与BE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买![]() 种图书花费了3000元,购买
种图书花费了3000元,购买![]() 种图书花费了1600元,A种图书的单价是
种图书花费了1600元,A种图书的单价是![]() 种图书的1.5倍,购买
种图书的1.5倍,购买![]() 种图书的数量比
种图书的数量比![]() 种图书多20本.
种图书多20本.
(1)求![]() 和
和![]() 两种图书的单价;
两种图书的单价;
(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了![]() 种图书20本和
种图书20本和![]() 种图书25本,共花费多少元?
种图书25本,共花费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,BD⊥AC于点D,AD=3.5cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,若在BD上有一动点E使PE+QE最短,则PE+QE的最小值为_____cm

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,△ABC是等边三角形,点D、E分别在边AB、BC上,且BD=BE,连接DE.
(1)求证:DE∥AC;
(2)将图①中的△BDE绕点B顺时针旋转,使得点A、D、E在同一条直线上,如图②,求∠AEC的度数;
(3)在(2)的条件下,如图③,连接CD,过点D作DM⊥BE于点M,在线段BM上取点N,使得∠DNE+∠DCE=180°.请探索三条线段EN,MN,EC之间的关系,并证明你的结论.
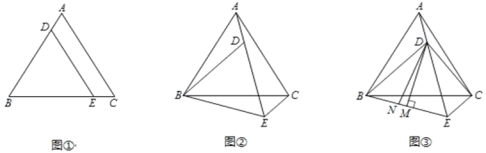
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A点的坐标为(m,3),AB⊥x轴于点B,tan∠OAB=![]() ,反比例函数y1=
,反比例函数y1=![]() 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.
(1)求反比例函数解析式;
(2)设直线OA的解析式为y2=nx,请直接写出y1<y2时,自变量x的取值范围 .
(3)如图2,若函数y=3x与y1=![]() 的图象的另一支交于点M,求△OMB与四边形OCDB的面积的比值.
的图象的另一支交于点M,求△OMB与四边形OCDB的面积的比值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com