
����Ŀ����ͼ����ABC�У���C=90��,AC=8cm,BC=6cm��������P�ӵ�C��ʼ����C��A��B��C��·���˶������ٶ�Ϊÿ��2cm�����˶���ʱ��Ϊt��.

��1����tΪ��ֵʱ��CP�ѡ�ABC���ܳ��ֳ���ȵ������֣�
��2����tΪ��ֵʱ��CP�ѡ�ABC������ֳ���ȵ������֣�
��3���ڣ�2��������£�������P��PE//BC������BC����һ��F��PE=CF������PF��
BE����̽��PF��BE��������ϵ.
���𰸡���1��t=6�룻��2��t=6.5�룻��3��������.
��������
��1�����ݹ��ɶ������AB���ɣ�
��2�����������ʽ�������з������ɣ�
��3������ȫ�������Σ�ͨ��ȫ�������ε��ж��������ʽ��н��.
�⣺

��1����ͼ1�� CP�ѡ�ABC���ܳ��ֳ���ȵ�������
�ߡ�C=90�㣬AC=8cm��BC=6cm
��![]()
�������AP=2t-8��BP=10-��2t-8��=10-2t+8=18-2t
��CP�ѡ�ABC���ܳ��ֳ���ȵ�������
��AC+AP=BC+BP����8+2t-8=6+18-2t�����t=6���룩��
��2����ͼ1����CP������ABC������ֳ���ȵ�������ʱ�������AB���ϣ�
��AP��BP�ֱ�Ϊ��APC����BPC�ĵױߣ����APC����BPC�й����ĸߣ�
�ߡ�APC����BPC�������ȣ�
��AP=BP=5��
��t=![]() =6.5���룩.
=6.5���룩.
��3����ͼ2������PC��
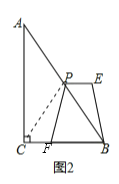
�ߵ�PΪֱ�ǡ�ABCб�ߵ��е㣬
��PC=PB����PCF=��PBC��
�֡�PE///BC��
���EPB=��PBC��
���EPB=��PCF��
�ڡ�PCF���BPE��
PC=PB ��PCF=��EPB CF=PE
���PCF�ա�BPE��SAS��
��PF=BE.


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90����AB=10cm��BC=6cm��������P�ӵ�C��ʼ��������C��A��B��C��·���˶������ٶ�Ϊÿ��2cm���������ʱ��Ϊt�룮
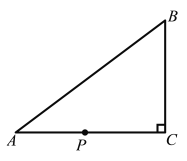
��1����գ�AC= cm��
��2������Pǡ���ڡ�ABC�Ľ�ƽ�����ϣ���t��ֵ��
��3����tΪ��ֵʱ����BPCΪ����������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AEƽ�֡�BAD���ֱ�BC��BD�ڵ�E��P������OE����ADC=60�㣬AB=![]() BC=1�������н��ۣ�
BC=1�������н��ۣ�
�١�CAD=30����BD=![]() ��Sƽ���ı���ABCD=ABAC��OE=
��Sƽ���ı���ABCD=ABAC��OE=![]() AD��S��APO=
AD��S��APO=![]() ����ȷ�ĸ����ǣ�������
����ȷ�ĸ����ǣ�������

A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��BCD�У���CBD=90�㣬BC=BD����A��CB���ӳ����ϣ���BA=BC����E��ֱ��BD���ƶ�������E������EF��EA����CD����ֱ���ڵ�F��

��1������E���߶�BD���ƶ�ʱ����ͼ��1����ʾ����֤��AE=EF��
��2������E��ֱ��BD���ƶ�ʱ����ͼ��2����ͼ��3����ʾ���߶�AE��EF����������������ϵ����ֱ��д����IJ��룬����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С���İְ�����ر߿���һ���ı�����������һЩ�߲ˣ��ְ���С������������ص�������Ա�����ֵ��С�����AB=4m,BC=3m,CD=13m.DA=12m.����֪��B=90�㣬ÿƽ����Ͷ���ʽ�80Ԫ��Ԥ�����ۺ��ֵÿƽ����480Ԫ���������������ܲ�����������?
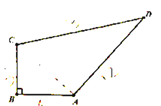
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() �ӵ�
�ӵ�![]() ������
������![]() �����˶�������
�����˶�������![]() ����
����![]() Ϊ�ߣ���
Ϊ�ߣ���![]() �Ҳఴ��ͼ��ʽ���ȱ�
�Ҳఴ��ͼ��ʽ���ȱ�![]() ������P�ӵ�E�˶�����Aʱ�����F�˶���·������
������P�ӵ�E�˶�����Aʱ�����F�˶���·������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���״�A������B���ߣ�ͬʱ�Ҵ�B������A���ߣ���ͼ�ཻ�ڵ�P�������߶���l1��l2�ֱ��ʾ�ס��Ҿ���B��·��y��km��������ʱ��x��h��֮��Ĺ�ϵ��
��1����������ߵ��ٶȣ�
��2����l1��l2�ı���ʽ��
��3����������ʱ�䵽��A�أ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MAN��һ�ּܣ�Ϊ��ʹ�ּܸ��Ӽ�̣���Ҫ�����ڲ�����һЩ�ֹ�BC,CD,DE���������ӵĸֹܳ��ȶ���AB��ȣ���ֻ�����������ĸֹ�4�������MAN�ķ�Χ____________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ADF����BCE�У���A=��B����D��E��F��C��ͬ��ֱ���ϣ�������������ϵʽ����AD=BC����DE=CF����BE��AF��

��1����������������ϵʽ��Ϊ��������һ����Ϊ���ۣ�д����������Ϊ��ȷ�����⣮�������д��������д��ʽ���磺����١�������ô�ۣ�
��2��ѡ��1������д����һ�����⣬˵������ȷ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com