
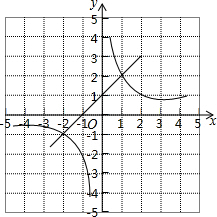
 一次函数y=kx+b与反比例函数y=$\frac{2}{x}$的图象如图所示,则使kx+b$>\frac{2}{x}$的x的取值范围是-2<x<0或x>1.
一次函数y=kx+b与反比例函数y=$\frac{2}{x}$的图象如图所示,则使kx+b$>\frac{2}{x}$的x的取值范围是-2<x<0或x>1. 分析 观察函数图象,先写出两函数的交点坐标,由于当-2<x<0或x>1时,直线y=kx+b都在y=$\frac{2}{x}$的图象上方,于是可得kx+b$>\frac{2}{x}$的x的取值范围.
解答 解:一次函数y=kx+b与反比例函数y=$\frac{2}{x}$的图象的交点坐标为(-2,-1)、(1,2),
所以当-2<x<0或x>1时,kx+b$>\frac{2}{x}$.
故答案为-2<x<0或x>1.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
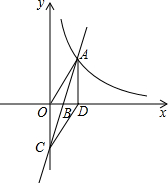 如图,直线y=kx-3(k>0)与x轴交于点B,与y轴的交于点C,与双曲线y=$\frac{k}{x}$在第一象限内的交点为点A,过点A作AD⊥x轴于点D,若四边形OADC是平行四边形,则k=3$\sqrt{2}$.
如图,直线y=kx-3(k>0)与x轴交于点B,与y轴的交于点C,与双曲线y=$\frac{k}{x}$在第一象限内的交点为点A,过点A作AD⊥x轴于点D,若四边形OADC是平行四边形,则k=3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
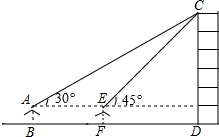 小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数)
小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com