
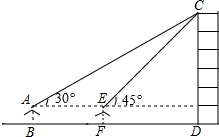
 小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数)
小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数) 分析 延长AE交CD于点G,设CG=xm,在直角△CGE中利用x表示出EG,然后在直角△ACG中,利用x表示出AG,根据AE=AG-EG即可列方程求得x的值,进而求出CD的长.
解答 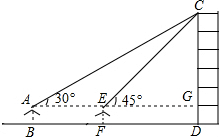 解:延长AE交CD于点G.设CG=xm,
解:延长AE交CD于点G.设CG=xm,
在直角△CGE中,∠CEG=45°,则EG=CG=xm.
在直角△ACG中,AG=$\frac{CG}{tan30°}$=$\sqrt{3}$xm.
∵AG-EG=AE,
∴$\sqrt{3}$x-x=30,
解得:x=15($\sqrt{3}$+1)≈15×2.732≈40.98(m).
则CD=40.98+1.5=42.48(m).
答:这栋建筑物CD的高度约为42m.
点评 本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.


科目:初中数学 来源: 题型:填空题
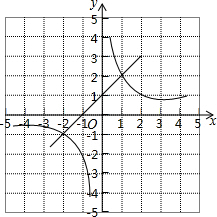 一次函数y=kx+b与反比例函数y=$\frac{2}{x}$的图象如图所示,则使kx+b$>\frac{2}{x}$的x的取值范围是-2<x<0或x>1.
一次函数y=kx+b与反比例函数y=$\frac{2}{x}$的图象如图所示,则使kx+b$>\frac{2}{x}$的x的取值范围是-2<x<0或x>1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )| A. | 6$\sqrt{3}$米 | B. | 6米 | C. | 3$\sqrt{3}$米 | D. | 3米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com