
分析 由等腰三角形腰是8,底是6,作出三角形的高AD和CE,根据三角形的面积公式得到CE=$\frac{BC•AD}{AB}$=$\frac{6×\sqrt{55}}{8}$=$\frac{3\sqrt{55}}{4}$,然后在直角△ACE中利用正弦函数的定义即可求出sin∠BAC的值.
解答 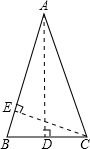 解:如图,等腰△ABC中,AB=AC=8,底边BC=6.
解:如图,等腰△ABC中,AB=AC=8,底边BC=6.
作AD⊥BC于D点,CE⊥AB于E点,则BD=$\frac{1}{2}$BC=3,
在Rt△ABD中,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{8}^{2}-{3}^{2}}$=$\sqrt{55}$,
∵S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$AB•CE,
∴CE=$\frac{BC•AD}{AB}$=$\frac{6×\sqrt{55}}{8}$=$\frac{3\sqrt{55}}{4}$,
∴sin∠BAC=$\frac{CE}{AC}$=$\frac{\frac{3\sqrt{55}}{4}}{8}$=$\frac{3\sqrt{55}}{32}$.
点评 本题考查了解直角三角形,等腰三角形的性质,三角形的面积,锐角三角函数定义,通过作辅助线构造直角三角形求出腰上的高CE是解题的关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
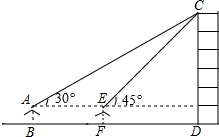 小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数)
小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414.结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙、丙、丁、戊五位同学参加一次节日活动,很幸运的是他们都得到了一件精美的礼品(如图),他们每人只能从其中一串的最下端取一件礼品,直到礼物取完为止,甲第一个取得礼物,然后乙、丙、丁、戊依次取得第2到第5件礼物,当然取法各种各样.
甲、乙、丙、丁、戊五位同学参加一次节日活动,很幸运的是他们都得到了一件精美的礼品(如图),他们每人只能从其中一串的最下端取一件礼品,直到礼物取完为止,甲第一个取得礼物,然后乙、丙、丁、戊依次取得第2到第5件礼物,当然取法各种各样.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在Rt△ABC中,∠C=90°,AB=4,∠ABC=30°,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOB=∠COB=120°,按下列要求画图:以点B为旋转中心,将△AOB绕点B逆时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),回答下列问题:
在Rt△ABC中,∠C=90°,AB=4,∠ABC=30°,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOB=∠COB=120°,按下列要求画图:以点B为旋转中心,将△AOB绕点B逆时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com