
分析 (1)直接利用单项式乘以多项式运算法则求出答案;
(2)直接利用乘法公式化简,进而利用多项式乘以多项式运算法则求出答案;
(3)首先利用级的乘方运算法则求出答案;
(4)结合幂的乘方运算法则以及同底数幂的乘法运算法则化简求出答案.
解答 解:(1)(x-y)(x2+xy+y2)
=x3+x2y+xy2-x2y-xy2-y3
=x3-y3;
(2)(3x-5)2-(2x+7)2
=(3x-5+2x+7)(3x-5-2x-7)
=(5x+2)(x-12)
=5x2-58x-24;
(3)(-$\frac{2}{3}$)2015×(1.5)2016
=(-$\frac{2}{3}$×1.5)2015×1.5
=-1.5;
(4)∵xm=3,xn=2,
∴x3m+2n=(xm)3×(xn)2=27×4=108.
点评 此题主要考查了整式的混合运算,正确掌握相关运算法则是解题关键.


科目:初中数学 来源: 题型:解答题
 根据要求完成下面的填空:
根据要求完成下面的填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△OAC是等腰直角三角形,直角顶点A在函数y=$\frac{9}{x}$(x>0)图象上,边OA交函数y=$\frac{1}{x}$(x>0)的图象于点B.求△ABC的面积.
如图,△OAC是等腰直角三角形,直角顶点A在函数y=$\frac{9}{x}$(x>0)图象上,边OA交函数y=$\frac{1}{x}$(x>0)的图象于点B.求△ABC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取男生、女生的人数相同,利用所得数据绘制如图统计图表:根据图表提供的信息,回答下列问题:
为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调查.已知抽取男生、女生的人数相同,利用所得数据绘制如图统计图表:根据图表提供的信息,回答下列问题:| 组别 | 身高 |
| A | x<155 |
| B | 155≤x<160 |
| C | 160≤x<165 |
| D | 165≤x<170 |
| E | x≥170 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
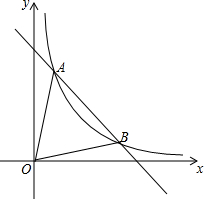 如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.
如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
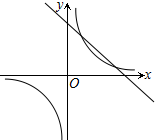 已知双曲线y=$\frac{6}{x}$和直线y=kx+4.
已知双曲线y=$\frac{6}{x}$和直线y=kx+4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com