
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据三角形的面积公式得到h=$\frac{ab}{c}$,由$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$,$\frac{1}{h}$=$\frac{c}{ab}$=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{ab}$,得到$\frac{1}{a}$+$\frac{1}{b}$≠$\frac{1}{h}$,①错误;②由于ab=ch,根据勾股定理得到$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$,②正确;③根据已知条件得到r=$\frac{1}{2}$(a+b-c),r1=$\frac{1}{2}$($\frac{ab}{c}$+$\frac{{b}^{2}}{c}$-b)=$\frac{b}{c}$r,r2=$\frac{1}{2}$($\frac{{a}^{2}}{c}$+$\frac{ab}{c}$-a)=$\frac{a}{c}$r,于是得到r12+r22=($\frac{b}{c}$r)2+($\frac{a}{c}$r)2=r2;③正确;④根据③中的条件即可得到r1+r2+r=$\frac{a+b+c}{c}$r=$\frac{a+b+c}{c}$•$\frac{a+b-c}{2}$=$\frac{ab}{c}$=h,④正确.
解答 证明:∵Rt△ABC中,∠ACB=90°,CD⊥AB于D,
∴由三角形面积公式得:S△ABC=$\frac{1}{2}$ab=$\frac{1}{2}$ch,
∴ab=ch,
∴h=$\frac{ab}{c}$,
①∵$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$,$\frac{1}{h}$=$\frac{c}{ab}$=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{ab}$,
∵a+b=$\sqrt{(a+b)^{2}}$,
∴$\frac{1}{a}$+$\frac{1}{b}$≠$\frac{1}{h}$,①错误;
②∵ab=ch,
∴a2b2=c2h2,
∴$\frac{1}{{a}^{2}{b}^{2}}$=$\frac{1}{{c}^{2}{h}^{2}}$,
∴$\frac{{c}^{2}}{{a}^{2}{b}^{2}}$=$\frac{1}{{h}^{2}}$
由勾股定理得:a2+b2=c2,
∴$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{{b}^{2}+{a}^{2}}{{a}^{2}{b}^{2}}$=$\frac{{c}^{2}}{{a}^{2}{b}^{2}}$,
∴$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$,②正确;
③∵△ACD、△BCD与△ABC的内切圆半径分别为r1,r2,r,
∴r=$\frac{1}{2}$(a+b-c),r1=$\frac{1}{2}$($\frac{ab}{c}$+$\frac{{b}^{2}}{c}$-b)=$\frac{b}{c}$r,r2=$\frac{1}{2}$($\frac{{a}^{2}}{c}$+$\frac{ab}{c}$-a)=$\frac{a}{c}$r,
∴r12+r22=($\frac{b}{c}$r)2+($\frac{a}{c}$r)2=r2;③正确;
④r1+r2+r=$\frac{a+b+c}{c}$r=$\frac{a+b+c}{c}$•$\frac{a+b-c}{2}$=$\frac{ab}{c}$=h,④正确.
点评 本题考查了三角形的内切圆与内心,三角形的面积公式,勾股定理,熟练掌握三角形的内心的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{x+1}{x-y}$=$\frac{-x+1}{x-y}$ | B. | $\frac{{x}^{2}+{y}^{2}}{x+y}$=x+y | ||
| C. | $\frac{0.5a+b}{0.2a-0.3b}$=$\frac{5a+10b}{2a-3b}$ | D. | $\frac{a-b}{a+b}$=$\frac{b-a}{b+a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运行区间 | 大人票价 | 学生票价 | |||
| 出发站 | 终点站 | 一等座 | 二等座 | 一等座 | 二等座 |
| 泉州 | 福州 | 65(元) | 54(元) | 65(元) | 40(元) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
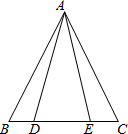 阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.
阅读并填空:如图,已知在△ABC中,AB=AC,点D、E在边BC上,且AD=AE,试说明BD=CE的理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一定是七次 | B. | 一定是四次 | C. | 一定是三次 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com