
| �������� | ����Ʊ�� | ѧ��Ʊ�� | |||
| ����վ | �յ�վ | һ���� | ������ | һ���� | ������ |
| Ȫ�� | ���� | 65��Ԫ�� | 54��Ԫ�� | 65��Ԫ�� | 40��Ԫ�� |
���� ��1�������ʦ�ͼҳ���������������һ��Ʊ�Ͷ���Ʊ��������������ʽ��
��2����μ����ʵ������ʦ��m�ˣ�ѧ����n�ˣ���ѧ���ҳ���2m�ˣ�������������Ա����һ�����Ķ���Ʊ������13650Ԫ�����������������Ʊ��ѧ��ȫ�������еġ�ѧ��Ʊ����������������8820Ԫ��������⣮
��3���ɣ�2��֪���в�����Ա�ܹ���210�ˣ�����ѧ����180�ˣ�������ѧ��Ʊ��180�ţ��У�x-180�������������������Ʊ����210-x����������һ��������Ʊ������Ʊ���ܷ��ò�����9000Ԫ�����в���ʽ��⣮
��� �⣺��1������һ��ƱΪ��65•3m=195m�� �������ƱΪ��54•3m=162m��
��2����μ����ʵ������ʦ��m�ˣ�ѧ����n�ˣ���ѧ���ҳ���2m�ˣ�������ã�
$\left\{\begin{array}{l}{195m+65n=13650}\\{54��3m+40n=8820}\end{array}\right.$����ã�$\left\{\begin{array}{l}{m=10}\\{n=180}\end{array}\right.$��
��2m=20��������Ϊ��10+20+180=210���ˣ�
�����飬��������
�𣺲μӻ��������Ϊ210�ˣ�
��3���ɣ�2��֪���в�����Ա�ܹ���210�ˣ�����ѧ����180�ˣ�
������ѧ��Ʊ��180�ţ��У�x-180�������������������Ʊ����210-x����������һ��������Ʊ��
���Ʊ���ܷ���=40��180+54��x-180��+65��210-x��=-11x+11130��
�����⣬�ã�-11x+11130��9000��
��ã�$x��193\frac{7}{11}$
��x����
��x�����ֵ��193
���� ���⿼������������������ؼ��Ǹ�����һ��Ʊ�Ͷ���Ʊ�ļ۸���Ϊ������ϵ���������Ȼ�����ʵ����Ʊ���ܷ����г�����ʽ����⣮


 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
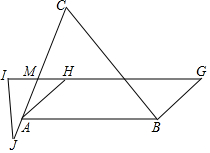 ��ͼ��ʾ����֪HΪ��ABC�Ĵ��ģ���G�����ı���ABGHΪƽ���ı��Σ�IΪֱ��GH�ϵĵ㣬AC��GI��M����IM=MH��JΪCA�ӳ�����һ�㣬��IJ=AH����֤��I��J��G��C�ĵ㹲Բ�������귨���÷֣�
��ͼ��ʾ����֪HΪ��ABC�Ĵ��ģ���G�����ı���ABGHΪƽ���ı��Σ�IΪֱ��GH�ϵĵ㣬AC��GI��M����IM=MH��JΪCA�ӳ�����һ�㣬��IJ=AH����֤��I��J��G��C�ĵ㹲Բ�������귨���÷֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{x}^{3}{y}^{2}}{{x}^{2}{y}^{3}}$=$\frac{x}{y}$ | B�� | $\frac{a-1}{b-1}$=$\frac{a}{b}$ | C�� | $\frac{a-b}{b-a}$=-1 | D�� | $\frac{1}{c}$+$\frac{2}{c}$=$\frac{3}{c}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���Ķ���Ȼ��ش����⣺
���Ķ���Ȼ��ش����⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| x | 0 | 1 | 2 |
| ax2 | 1 | ||
| ax2+bx+c | 5 | 6 |
| A�� | 4.5 | B�� | 9.5 | C�� | -1.5 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com