练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

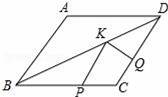
    如图，菱形ABCD中，AB=4，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为　．


    2　【考点】轴对称-最短路线问题；菱形的性质．

    【分析】根据轴对称确定最短路线问题，作点P关于BD的对称点P′，连接P′Q与BD的交点即为所求的点K，然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK+QK的最小值，然后求解即可．

    【解答】解：如图，∵AB=4，∠A=120°，

    ∴点P′到CD的距离为4×=2，

    ∴PK+QK的最小值为2．

    故答案为：2．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    若a－b＜0，则下列各式中一定正确的是（  ）

     A、a＞b  B、ab＞0  C、   D、－a＞－b

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    写出二次项系数为5，以x1=1,x2=2为根的一元二次方程　　　　　　。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AB是⊙O的直径，C是的中点，CE⊥AB于E，BD交CE于点F．

    （1）求证：CF=BF；

    （2）若CD=6，AC=8，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图中的虚线网格我们称为正三角形网格，它的每一个小三角形都是边长为1个单位长度的正三角形，这样的三角形称为单位正三角形．

    （1）图①中，已知四边形ABCD是平行四边形，求△ABC的面积和对角线AC的长；

    （2）图②中，求四边形EFGH的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，矩形纸片ABCD，AB=3，AD=5，折叠纸片，使点A落在BC边上的E处，折痕为PQ，当点E在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点E在BC边上可移动的最大距离为（　　）

    A．1    B．2    C．4    D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知a∥b，小亮把三角板的直角顶点放在直线b上，若∠1=40°，则∠2的度数为（　　）

    A．30° B．40° C．45° D．50°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分解因式：a3b﹣9ab3=　                  

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    这样铺地板：第一块铺2块，如图1，第二次把第一次的完全围起来，如图2；第三次把第二次的完全围起来，如图3；…依次方法，铺第5次时需用　　木块才能把第四次所铺的完全围起来．

    查看答案和解析>>

    同步练习册答案