
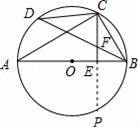
如图,AB是⊙O的直径,C是
 的中点,CE⊥AB于E,BD交CE于点F.
的中点,CE⊥AB于E,BD交CE于点F.
(1)求证:CF=BF;
(2)若CD=6,AC=8,求⊙O的半径.


【考点】圆周角定理;勾股定理;圆心角、弧、弦的关系.
【分析】(1)首先延长CE交⊙O于点P,由垂径定理可证得∠BCP=∠BDC,又由C是
 的中点,易证得∠BDC=∠CBD,继而可证得CF=BF;
的中点,易证得∠BDC=∠CBD,继而可证得CF=BF;
(2)由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠ACB=90°,然后由勾股定理求得AB的长,继而求得答案.
【解答】(1)证明:延长CE交⊙O于点P,
∵CE⊥AB,
∴
 =
=
 ,
,
∴∠BCP=∠BDC,
∵C是
 的中点,
的中点,
∴CD=CB,
∴∠BDC=∠CBD,
∴∠CBD=∠BCP,
∴CF=BF;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵CD=6,AC=8,
∴BC=6,
在Rt△ABC中,AB=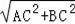
 =10,
=10,
∴⊙O的半径为5.



 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
用配方法解方程x2+8x-7=0,则配方正确的是( )
A.(x+4)2=23 B.(x﹣4)2=23 C.(x﹣8)2=49  D.(x+8)2=64
D.(x+8)2=64
查看答案和解析>>
科目:初中数学 来源: 题型:
作为宁波市政府民生实事之一的公共自行车建设工作已基本完成,某部门对今年4月份中的7天进行了公共自行车日租车量的统计,结果如图:


(1)求这7天日租车量的众数、中位数和平均数;
(2)用(1)中的平均数估计4月份(30天)共租车多少万车次;
(3)市政府在公共自行车建设项目中共投入9600万元,估计2014年共租车3200万车次,每车次平均收入租车费0.1元,求2014年租车费收入占总投入的百分率(精确到0.1%).
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com