
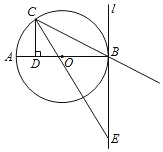
【题目】如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB于D,AD=2,CD=4.∠BCD的角平分线CE与过点B的切线l交过点E.
(1)求⊙O半径的长;
(2)求点E到直线BC的距离.
【答案】(1)5;(2)8;
【解析】
(1)如图1中,连接OC,设⊙O的半径为r.在Rt△CDO中,利用勾股定理即可解决问题.
(2)如图2中,过点E作EF⊥CD,垂足为点F,EG⊥CB,垂足为G,则∠EFD=90°,只要证明四边形BDFE是矩形,求出EF,利用角平分线的性质可得EG=EF即可解决问题.
(1)如图1中,连接OC,设⊙O的半径为r.

∵AD=2,OD=r﹣2,
∵CD⊥AB,
∴∠CDO=90°,
在Rt△CDO中,∵CD2+DO2=CO2,
∴42+(r﹣2)2=r2,
∴r=5,
⊙O的半径为5.
(2)如图2中,过点E作EF⊥CD,垂足为点F,EG⊥CB,垂足为G,则∠EFD=90°,

∵直线l切⊙O于B,
∴AB⊥l,
∴∠DBE=90°,
∵CD⊥AB,
∴∠BDF=90°,
∴四边形BDFE是矩形,
∴EF=BO+OD=8,
∵点E在∠BCD的平分线上,
∴EG=EF=8.
∴点E到直线BC的距离为8.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】一次函数y=kx﹣1的图象经过点P,且y的值随x值的增大而增大,则点P的坐标可以为( )
A. (﹣5,3) B. (1,﹣3) C. (2,2) D. (5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
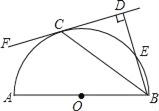
【题目】如图,AB是半圆O的直径,C是半圆O上的一点,CF切半圆O于点C,BD⊥CF于为点D,BD与半圆O交于点E.
(1)求证:BC平分∠ABD.
(2)若DC=8,BE=4,求圆的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,AB=2,点C在![]() 上运动,且∠ACB=30°.
上运动,且∠ACB=30°.

(1)求⊙O的半径;
(2)设点C到直线AB的距离为x,图中阴影部分的面积为y,求y与x之间的函数关系,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 点在直线
点在直线![]() 上,过点
上,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,以点
,以点![]() 为直角顶点,
为直角顶点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
的右侧作等腰直角![]() ,再过点
,再过点![]() 作
作![]() 轴,分别交直线
轴,分别交直线![]() 和
和![]() 于
于![]() 两点,以点
两点,以点![]() 为直角项点,
为直角项点,![]() 为直角边在
为直角边在![]() 的右侧作等腰直角
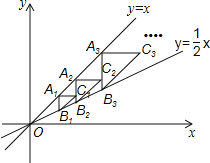
的右侧作等腰直角![]() …,按此规律进行下去,则等腰直角
…,按此规律进行下去,则等腰直角![]() 的面积为___. (用含正整数
的面积为___. (用含正整数![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
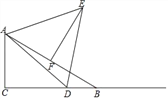
【题目】在Rt△ABC中,∠C=90°,∠B=30°,AB=10,点D是射线CB上的一个动点,△ADE是等边三角形,点F是AB的中点,连接EF.
(1)如图,点D在线段CB上时,
①求证:△AEF≌△ADC;
②连接BE,设线段CD=x,BE=y,求y2﹣x2的值;
(2)当∠DAB=15°时,求△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=![]() ,以O为圆心,OC为半径作
,以O为圆心,OC为半径作![]() ,交OB于E点.
,交OB于E点.
(1)求⊙O的半径OA的长;
(2)计算阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,AB是⊙O的直径,G为弦AE的中点,连接OG并延长交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为5,tanA=![]() ,求FD的长.
,求FD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com