
【题目】(1)如图①,在矩形ABCD中,AB=4,AD=10,在BC边上是否存在点P,使∠APD=90°,若存在,请用直尺和圆规作出点P并求出BP的长.(保留作图痕迹)
(2)如图②,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E、F分别为AB,AC的中点,当AD=6时,BC边上是否存在一点Q,使∠EQF=90°,求此时BQ的长.


【答案】(1)2或8;(2)存在,3+![]() .
.
【解析】试题分析:(1)以AD为直径画圆与BC交于点P1、P2,则点P1、P2为所求点;由矩形的性质得到AD=BC=10,AB=CD=4根据三角形相似即可解出;
(2)由三角形的中位线得到EF∥BC,EF=![]() BC=6,根据EF与BC间距离为3,推出以EF为直径的 O与BC相切,得出BC上符合条件的点Q只有一个,记 O与BC相切于点Q,连接OQ,过点E作EG⊥BC,垂足为G,证出四边形EOQG为正方形,由勾股定理即可求出.
BC=6,根据EF与BC间距离为3,推出以EF为直径的 O与BC相切,得出BC上符合条件的点Q只有一个,记 O与BC相切于点Q,连接OQ,过点E作EG⊥BC,垂足为G,证出四边形EOQG为正方形,由勾股定理即可求出.
解:(1)如图①所示,点P1、P2为所求的点;(保留作图痕迹)
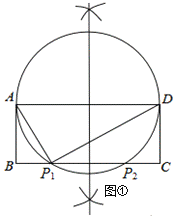
在矩形ABCD中,连接AP1、DP1,AD=BC=10,AB=CD=4,
设BP1=x,则P1C=10﹣x,
∵∠AP1D=90°,∴∠AP1B+∠CP1D=90°,
∵∠BAP1+∠AP1B=90°,∴∠BAP1=∠CP1D,
又∵∠B=∠C=90°,∴△ABP1∽△P1CD,
∴![]() ,∴
,∴![]() ,
,
解得:x1=2,x2=8,∴BP的长是2或8
(2)如图②,
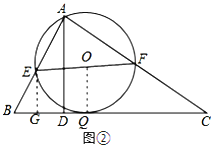
∵EF分别为AB、AC的中点,∴EF∥BC,EF=![]() BC=6,
BC=6,
∵AD=6,AD⊥BC,∴EF与BC间距离为3,
∴以EF为直径的⊙O与BC相切,
∴BC上符合条件的点Q只有一个,记⊙O与BC相切于点Q,
连接OQ,过点E作EG⊥BC,垂足为G,
∴EG=OE=3,∴四边形EOQG为正方形,
在Rt△EBG中,∠B=60°,EG=3,∴BG=![]() ,∴BQ=3+
,∴BQ=3+![]() .
.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.
(1)直接写出线段AD及⊙O半径的长;
(2)设PH=x,PC=y,求y关于x的函数关系式;
(3)当PH与⊙O相切时,求相应的y值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使锐角△AOB的面积等于3.求点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABM=30°,AB=20,C是射线BM上一点.
(1)在下列条件中,可以唯一确定BC长的是 ;(填写所有符合条件的序号)
①AC=13;②tan∠ACB=![]() ;③△ABC的面积为126.
;③△ABC的面积为126.
(2)在(1)的答案中,选择一个作为条件,画出示意图,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我们所学的课本中,多项式与多项式相乘可以用几何图形的面积来表示.例如,(2a+b)(a+b)=2a2+3ab+b2就可以用图(1)来表示.请你根据此方法写出图(2)中图形的面积所表示的代数恒等式:____________.

【答案】(a+2b)(2a+b)=2a2+5ab+2b2
【解析】试题分析:图②的面积可以用长为a+a+b,宽为b+a+b的长方形面积求出,也可以由四个正方形与5个小长方形的面积之和求出,表示出即可.
解:根据图形列得:(a+2b)(2a+b)=2a2+5ab+2b2.
故答案为:(a+2b)(2a+b)=2a2+5ab+2b2.
考点:多项式乘多项式.
点评:此题考查了多项式乘以多项式法则,熟练掌握法则是解本题的关键.
【题型】填空题
【结束】
18
【题目】若一个正整数能表示为两个正整数的平方差,则称这个正整数为“智慧数”(如3=22-12,16=52-32,则3和16是智慧数).已知按从小到大的顺序构成如下数列:3,5,7,8,9,11,12,13,15,16,17,19,20,21,23,24,25,…则第2 013个“智慧数”是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=![]() ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
【答案】(1)原式= 2a2+b2=2+2=4;(2)原式=4.
【解析】试题分析:(1)利用完全平方公式展开,化简,代入求值. (2) 利用完全平方公式展开,化简,整体代入求值.
解:(1)原式=a2-2ab+a2+2ab+b2=2a2+b2.
当a=-1,b=![]() 时,原式=2+2=4.
时,原式=2+2=4.
(2)原式=2x2-3x+1-(x2+2x+1)+1=x2-5x+1=3+1=4.
【题型】解答题
【结束】
22
【题目】已知化简(x2+px+8)(x2-3x+q)的结果中不含x2项和x3项.
(1)求p,q的值.
(2)x2-2px+3q是否是完全平方式?如果是,请将其分解因式;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
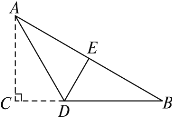
【题目】如图,有一块直角三角形纸片,两直角边AC=6 cm,BC=8 cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com