
【题目】已知:如图,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使锐角△AOB的面积等于3.求点B的坐标.

【答案】(1)y=x2-3x,(2)(4,4).
【解析】试题分析:(1)将原点坐标代入抛物线中即可求出k的值,也就得出了抛物线的解析式.
(2)根据(1)得出的抛物线的解析式可得出A点的坐标,也就求出了OA的长,根据△OAB的面积可求出B点纵坐标的绝对值,然后将符合题意的B点纵坐标代入抛物线的解析式中即可求出B点的坐标,然后根据B点在抛物线对称轴的右边来判断得出的B点是否符合要求即可.
试题解析:①∵函数的图象与x轴相交于O,
∴0=k+1,
∴k=-1,
∴y=x2-3x,
②假设存在点B,过点B做BD⊥x轴于点D,
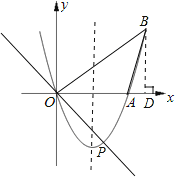
∵△AOB的面积等于6,
∴![]() AOBD=6,
AOBD=6,
当0=x2-3x,
x(x-3)=0,
解得:x=0或3,
∴AO=3,
∴BD=4
即4=x2-3x,
解得:x=4或x=-1(舍去).
又∵顶点坐标为:(1.5,-2.25).
∵2.25<4,
∴x轴下方不存在B点,
∴点B的坐标为:(4,4).


科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,OB、OC是∠ABC、∠ACB的角平分线;
(1)填写下面的表格.
∠A的度数 | 50° | 60° | 70° |
∠BOC的度数 |
(2)试猜想∠A与∠BOC之间存在一个怎样的数量关系,并证明你的猜想;
(3)如图2,△ABC的高BE、CD交于O点,试说明图中∠A与∠BOD的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图像进行探究。
(1)填空甲、乙两地之间的距离为_______千米;
(2)请解释图中的点B的实际意义;________________
(3)直接写出慢车速度_________,快车的速度___________
(4)求线段BC所表示的y与x之间的函数关系式,并直接写出自变量x的取值范围;

查看答案和解析>>
科目:初中数学 来源: 题型:
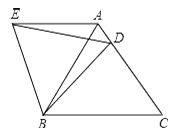
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列四个结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△AED的周长是9.其中正确的结论是__(把你认为正确结论的序号都填上.)
查看答案和解析>>
科目:初中数学 来源: 题型:
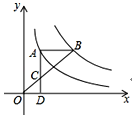
【题目】如图,点A在双曲线y=![]() 上,点B在双曲线y=
上,点B在双曲线y=![]() (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k=__.
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在矩形ABCD中,AB=4,AD=10,在BC边上是否存在点P,使∠APD=90°,若存在,请用直尺和圆规作出点P并求出BP的长.(保留作图痕迹)
(2)如图②,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E、F分别为AB,AC的中点,当AD=6时,BC边上是否存在一点Q,使∠EQF=90°,求此时BQ的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一枚均匀的正四面体,四个面上分别标有数字1,2,3,4,小红随机地抛掷一次,把着地一面的数字记为x;另有三张背面完全相同,正面上分别写有数字-2,-1,1的卡片,小亮将其混合后,正面朝下放置在桌面上,并从中随机地抽取一张,把卡片正面上的数字记为y;然后他们计算出S=x+y的值.
(1)用树状图或列表法表示出S的所有可能情况;
(2)分别求出当S=0和S<2时的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com