
【题目】如图1,在△ABC中,OB、OC是∠ABC、∠ACB的角平分线;
(1)填写下面的表格.
∠A的度数 | 50° | 60° | 70° |
∠BOC的度数 |
(2)试猜想∠A与∠BOC之间存在一个怎样的数量关系,并证明你的猜想;
(3)如图2,△ABC的高BE、CD交于O点,试说明图中∠A与∠BOD的关系.

【答案】(1)表格见解析(2)∠BOC=90°+![]() ∠A(3)证明见解析
∠A(3)证明见解析
【解析】(1)
∠A的度数 | 50° | 60° | 70° |
∠BOC的度数 | 115° | 120° | 125° |
(2)猜想:∠BOC=90°+![]() ∠A.
∠A.
理由:∵在△ABC中,OB、OC是∠ABC、∠ACB的角平分线;
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∵∠ABC+∠ACB=180°﹣∠A,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣![]() ∠A,
∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(90°﹣![]() ∠A)=90°+
∠A)=90°+![]() ∠A.
∠A.
(3)证明:∵△ABC的高BE、CD交于O点,
∴∠BDC=∠BEA=90°,
∴∠ABE+∠BOD=90°,∠ABE+∠A=90°,
∴∠A=∠BOD.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】若x0是方程ax2+2x+c=0(a≠0)的一个根,设M=1﹣ac,N=(ax0+1)2 , 则M与N的大小关系正确的为( )
A.M>N
B.M=N
C.M<N
D.不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AC是ABCD的一条对角线,过AC中点O的直线分别交AD,BC于点E,F.
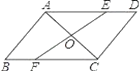
(1)求证:AE=CF;
(2)连接AF,CE.
①当EF和AC满足条件 时,四边形AFCE是菱形;
②若AB=1,BC=2,∠B=60°,则四边形AFCE为矩形时,EF的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有3个球,球上分别标有数字0,1,2,这些球除了数字外其余都相同,甲、以两人玩摸球游戏,规则如下:先由甲随机摸出一个球(不放回),再由乙随机摸出一个球,两人摸出的球所标的数字之和为偶数时则甲胜,和为奇数时则乙胜.
(1)用画树状图或列表的方法列出所有可能的结果;
(2)这样的游戏规则是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P在射线AC上运动,过点P作PH⊥AB,垂足为H.
(1)直接写出线段AD及⊙O半径的长;
(2)设PH=x,PC=y,求y关于x的函数关系式;
(3)当PH与⊙O相切时,求相应的y值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使锐角△AOB的面积等于3.求点B的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com