Question

【题目】AC是ABCD的一条对角线，过AC中点O的直线分别交AD，BC于点E，F．

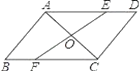
（1）求证：AE=CF；

（2）连接AF，CE．

①当EF和AC满足条件 时，四边形AFCE是菱形；

②若AB=1，BC=2，∠B=60°，则四边形AFCE为矩形时，EF的长是 ．

Answer 1

【答案】（1）证明见解析；（2）①EF⊥AC，理由见解析；②

【解析】试题分析：（1）由平行四边形的性质可知OA=OC，∠AEO=∠OFC，∠EAO=∠OCF，证出△AOE≌△COF，即可得出AE=CF．

（2）①先证明四边形AFCE是平行四边形，由EF⊥AC，即可得出四边形AFCE是菱形；②由矩形的性质得出EF=AC，∠AFB=∠AFC=90°，求出AF、CF，由勾股定理求出AC，即可得出EF的长．

试题解析：（1）证明：∵AD∥BC，

∴∠EAO=∠FCO.

∵O是AC的中点，

∴OA=OC，

在△AOE和△COF中，

，

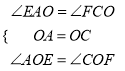∴△AOE≌△COF(ASA).

∴AE=CF.

(2)①当EF和AC满足条件EF⊥AC时，四边形AFCE是菱形；理由如下：如图所示：

∵AE∥CF，AE=CF，

∴四边形AFCE是平行四边形，

又∵EF⊥AC，

∴四边形AFCE是菱形；

②若四边形AFCE为矩形，

则EF=AC，∠AFB=∠AFC=90°，

∵AB=1，BC=2,∠B=60°，

∴∠BAF=30°，

∴BF=AB=，

∴AF=BF=，CF=2=，

∴AC==，

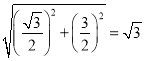∴EF=；

故答案为：