
����Ŀ���˿���ij�ڽ�������һ���ڼ䵽�����̳�����յ�����ӪҵԱ�����µ�һ�ζԻ���
�˿���ij��AƷ�ƵĿյ�ȥ�����������ڼ�۸�ͦ�ߣ���α��˶��ˣ�һ�ν��۷��Ⱦʹﵽ19%���Dz������������⣿
ӪҵԱ������һ�ν��ۣ����ǵڶ��ν��ۣ����괺���ڼ��Ѿ�����һ�μۣ����ν��۵ķ�����ͬ�����������۵Ŀյ��������Ǻܺõģ�������AƷ��ϵ�пյ���������һ���ģ�
�˿���ij�����ǵ�λ��ͬ��Ҳ����AƷ�ƵĿյ������Ż�������
ӪҵԱ���У��뿴������AƷ��ϵ�пյ����Żݰ취����

�������϶Ի���AƷ��ϵ�пյ����۵��Żݰ취������ش��������⣺
��1����AƷ��ϵ�пյ�ƽ��ÿ�ν��۵İٷ��ʣ�
��2������Ϊ�˿���ij���ߣ�ѡ�������Żݸ����㣬��˵��Ϊʲô��
���𰸡���1��AƷ��ϵ�пյ�ƽ��ÿ�ν��۵İٷ���Ϊ10%��
��2����AƷ��ϵ�пյ���ijһ�ͺŵļ۸�Ϊÿ̨��3000Ԫʱ��Ӧѡ��������
��AƷ��ϵ�пյ���ijһ�ͺŵļ۸�Ϊÿ̨3000Ԫʱ�����ַ���������ѡ��
��AƷ��ϵ�пյ���ijһ�ͺŵļ۸�Ϊÿ̨��3000Ԫʱ��Ӧѡ����һ��
�������������������1����AƷ��ϵ�пյ�ƽ��ÿ�ν��۵İٷ���Ϊx��ԭ��Ϊa�����������ʵ�һ�㹫ʽ�����г����̽�����⣻
��2�����˿���ij����Ҫ���AƷ��ϵ�пյ���ijһ�ͺŵļ۸�Ϊÿ̨xԪ��Ȼ��ֱ���x��ʾ���ַ����ĺ�����ϵʽ�����ŷ�������ۣ���ͬ����ķ����շѣ��Ƚϴ�С���ɵõ����ۣ�
�����������1����AƷ��ϵ�пյ�ƽ��ÿ�ν��۵İٷ���Ϊx��ԭ��Ϊa��
�������⣬��a��1-x��2=a��1-19%����
���x1=1.9���������⣬��ȥ����x2=0.1=10%��
��2�����˿���ij����Ҫ���AƷ��ϵ�пյ���ijһ�ͺŵļ۸�Ϊÿ̨xԪ��
�����Żݷ���һÿ̨��֧��y1Ԫ�������Żݷ�����ÿ̨��֧��y2Ԫ��
��y1=0.95x+90��y2=0.98x��
��y1��y2ʱ��x��3000��Ԫ������ʱӦѡ��������
��y1=y2ʱ��x=3000��Ԫ������ʱѡ���ַ�����һ����
��y1��y2ʱ��x��3000��Ԫ������ʱӦѡ����һ��
�𣺣�1��AƷ��ϵ�пյ�ƽ��ÿ�ν��۵İٷ���Ϊ10%��
��2����AƷ��ϵ�пյ���ijһ�ͺŵļ۸�Ϊÿ̨��3000Ԫʱ��Ӧѡ��������
��AƷ��ϵ�пյ���ijһ�ͺŵļ۸�Ϊÿ̨3000Ԫʱ�����ַ���������ѡ��
��AƷ��ϵ�пյ���ijһ�ͺŵļ۸�Ϊÿ̨��3000Ԫʱ��Ӧѡ����һ��


 ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д� һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
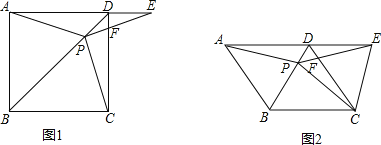
����Ŀ����ͼ1��������ABCD�У�P�ǶԽ���BD�ϵ�һ�㣬��E��AD���ӳ����ϣ���PA=PE��PE��CD��F.
��1��֤����PC=PE��
��2�����CPE�Ķ�����
��3����ͼ2����������ABCD��Ϊ����ABCD�������������䣬����ABC=120��ʱ������CE����̽���߶�AP���߶�CE��������ϵ����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ʽA=��x+1��2����x2��4y����
��1���������ʽA��
��2����x+2y=1����A��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ְ־�Ӫ��ˮ�������һ�������ȴ�ˮ���������ϳ�����С����������ͼ��㣬��������ˮ��ÿ�µ�������y(ǧ��)�����۵���x��Ԫ��֮�������һ�κ�����ϵ��y=-10x+500(20��x��50)�����������ǵ�һ�ζԻ���
С��������Ҫ�Ǹ������ۼ�����ˮ���Ľ����Ƕ��٣��Ҿ��ܰ���Ԥ��ö���Ϣ�أ���
�ְ֣����ۼ�����ˮ���Ľ�����ÿǧ��20Ԫ��
�������㣬Ҳ�����һ��С����Ҫ������������⣺
��1����ÿ�»������w(Ԫ�������۵���x��Ԫ���ĺ���������������ı���ʽ��
��2�������۵���Ϊ����Ԫʱ��ÿ�¿ɻ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��AC��ABCD��һ���Խ��ߣ���AC�е�O��ֱ�߷ֱ�AD��BC�ڵ�E��F��
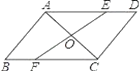
��1����֤��AE=CF��
��2������AF��CE��
�ٵ�EF��AC�������� ʱ���ı���AFCE�����Σ�
����AB=1��BC=2����B=60�������ı���AFCEΪ����ʱ��EF�ij��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�1������֯�༶�����ᣬ������齱���ڣ�ÿ��ͬѧ����һ�γ齱���ᣬ�齱�������£���һ���˿����е���Ϊ��2������3������3������5������6���������Ʊ��泯��ϴ�ȣ��ȴ��г��1���ƣ��ٴ����µ�4�����г��1���ƣ���¼�����Ƶ�����Żأ����һ�γ齱����ÿ�γ�������Ƶ���֮��Ϊ![]() ��������Ҫ��ȷ�����
��������Ҫ��ȷ�����

��1�����б�����״ͼ�ķ��������ͬѧ���һ�Ƚ��ĸ��ʣ�
��2���Ƿ�ÿ�γ齱�����Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ڽ�һ������ε��ڽ�������ʱ��������һ���ڽǶ����һ�Σ�����صõ��ڽǺ�Ϊ840�������������εı�����___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.a2a3=a6
B.����y2��3=y6
C.��m2n��3=m5n3
D.��2x2+5x2=3x2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com