
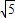 ,求垂线段OE的长.
,求垂线段OE的长.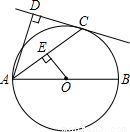
 (1)证明:连接OC.
(1)证明:连接OC. ,则由勾股定理得,
,则由勾股定理得, =8.
=8. AC=2
AC=2 .
. =
= .
. =
= =
= .即垂线段OE的长为
.即垂线段OE的长为 .
.

 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
 如图是9×7的正方形点阵,其水平方向和竖直方向的两格点间的长度都为1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:
如图是9×7的正方形点阵,其水平方向和竖直方向的两格点间的长度都为1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 23、如图是9×7的正方形点阵,其水平方向和竖直方向相邻的两格点间的长度都是1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:
23、如图是9×7的正方形点阵,其水平方向和竖直方向相邻的两格点间的长度都是1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:查看答案和解析>>
科目:初中数学 来源:2012年人教版初中数学九年级上25.2列举法求概率练习卷(解析版) 题型:解答题
如图是9×7的正方形点阵,其水平方向和竖起直方向的两格点间的长度都为1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:

(1)请在图中画出以AB为边且面积为2的一个网格三角形;
(2)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形的面积为2的概率;
(3)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形为直角三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是9×7的正方形点阵,其水平方向和竖起直方向的两格点间的长度都为1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:
如图是9×7的正方形点阵,其水平方向和竖起直方向的两格点间的长度都为1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:查看答案和解析>>
科目:初中数学 来源:2010年内蒙古呼和浩特市中考数学预测试卷(二)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com